Deep learning, ИИ и что там делает математика

Беседа Ксении Королёвой с математиком Алексеем Соляником, профессором Одесского политехнического университета, с 2009 года путешествующим и живущим на своем тримаране по всему миру¹, об искусственном интеллекте, квантовых компьютерах и теории хаоса. Аудиозапись: youtu.be/ycJtKHLHtQ8

— Что для вас как математика искусственный интеллект и что такое глубокое обучение (deep learning)?

— Для меня как математика это некоторая математическая конструкция, не очень сложная. Можно говорить, из чего она состоит: там есть слои, состоящие из нейронов (node), которые являются простейшими микропроцессорами, соединенными определенным образом. Но суть в том, что мы ищем некоторые веса, а это по сути теория приближений, то, что в математике называется теорией аппроксимации. Выбираются какие-то веса, прогоняются какие-то тесты и после этого сеть настраивается на нужные значения. Ну, точнее, предполагается, что она настраивается. В этом состоит искусственный интеллект для математика. Есть некоторая математическая конструкция, которая реализуется.

— А какие области математики применимы для глубокого обучения?

— «Основано на чем», — лучше так сказать, в некотором смысле это столпы, на которых стоит вся наука. Во-первых, это линейная алгебра, затем математический анализ. Линейная алгебра, потому что мы работаем с большими массивами данных. Эти данные представляются векторами в многомерном пространстве, или матрицами.

Чтобы объяснить, как используется математический анализ, прежде надо объяснить идею, на которой основан принцип работы нейросети. Как правило, любой процесс от чего-то зависит. Во-первых, от времени, но время — это общая переменная, которая меняется, а есть еще масса факторов, которые влияют на процесс, что в экономике, что в метеорологии… Эти факторы… их много, и сложность понимания мира состоит в том, что мы не знаем всех этих факторов, — это во-первых, а во-вторых, не знаем закона, в соответствии с которым эти факторы влияют на изучаемый процесс, т. е. мы не знаем динамики. Но иногда мы знаем, и это составляет научное открытие. Например, законы Ньютона: они описывают движение планет вокруг Солнца и предсказывают достаточно точно поведение этих планет. Эти законы были эмпирически открыты Иоганном Кеплером, а потом законы Кеплера были выведены как следствия из открытого Ньютоном закона всемирного тяготения. И они правильно предсказывают поведение системы. Но во многих задачах эти законы неизвестны. Например, в экономике эти законы очень приблизительны и достаточно плохо описывают реальные события. В медицине по-прежнему эти законы неизвестны; много еще можно назвать наук, в которых эти «законы» — пока лишь только предположения и не совсем адекватно описывают всю систему. В психологии, например. Ну а задача искусственного интеллекта — не зная закона, смоделировать явление.

Возникает вопрос: как это сделать? Делается это в некотором смысле очень просто. Вам нужно знать, какие именно факторы и насколько сильно влияют на исход. Некоторые вообще не влияют, некоторые — влияют наиболее существенно. В зависимости от этого расставляются так называемые веса в этой нейронной сети. Так вот, эти веса — фактически какие-то числовые коэффициенты — отражают степени влияния определенных факторов.

И далее возникает вопрос: как же их подбирать правильно? Если подбирать случайно, то это займет очень много времени. Иногда так и делают — когда ничего больше не остается, а иногда поиск ведут более целенаправленно. Так приблизительно и происходят научные открытия: ищут эти факторы — и наконец находят. Ньютон обнаружил, что движение Земли вокруг Солнца зависит от масс тяготеющих тел и от расстояния между ними. Ну а, например, от поведения кошки в каком-то доме вряд ли зависит характер движения Земли. Так вот, когда он эти факторы нашел и описал динамику, то в этом и состояло научное открытие.

Так же действует искусственный интеллект: он прогоняет много разных примеров и после этого выбирает те веса, с которыми нейросеть правильно отражает явление, вернее сказать, ее выход (output) правильно отражает явление. Но как искать эти веса? Есть такой метод градиентного спуска: вы просто стараетесь двигаться по самому короткому пути, и здесь нужен математический анализ. Я перехожу ко «второму столпу». Математический анализ — это поиск производных, поиск градиента и правильный выбор направления, в котором надо двигаться, чтобы эти веса правильно подбирать. Далее вопросы оптимизации, всё, что связано с оптимальным управлением, с поиском оптимальных решений, в том числе и вариационное исчисление, и, наверное, теория вероятности во многом. Потому что сейчас в нейронных сетях применяются вероятностные алгоритмы. Вот такие четыре основных математических бэкграунда искусственного интеллекта.

— Насколько теории хаоса и динамических систем применимы для прогнозирования событий? И что ограничивает эту систему? Например, у нас есть квантовая физика, и она везде работает, но появляется фигура наблюдателя и всё рушит. И вопрос: что происходит здесь?

— Давайте со второго вопроса — того, что касается квантовой механики. То, о чем вы говорите, — это известный принцип неопределенности Гейзенберга. Это немножко из другой области, можно сказать, даже более модной. Это создание квантовых компьютеров. Эти вещи, которые имеют отношение к принципу неопределенности Гейзенберга, и, собственно говоря, он очень сильно мешает их создавать. Из-за того, что этот принцип лежит в основе квантовой механики, очень сложно создавать квантовые компьютеры. Сегодня существуют модели — но они еще очень далеки от реальных суперкомпьютеров. Имеется в виду, что они могут считать, но считают пока очень маленькие массивы чисел. Ограничения накладываются технологиями, а не теорией, и это не связано с искусственным интеллектом. Квантовые компьютеры — это просто другой принцип построения компьютера, информация там в кубитах считается, и всё это как раз основано на принципе неопределенности Гейзенберга; квантовый компьютер оперирует не просто дискретными значениями «1» и «0» — он имеет дело с некоторым вероятностным облаком, да еще и в комплексном пространстве. Но после создания этих компьютеров всё сразу изменится очень резко. Я имею в виду — после их реального запуска. Потому что они, например, смогут раскрывать шифры. Сейчас уже известны алгоритмы для квантовых компьютеров, которые способны факторизовать (раскладывать на простые сомножители) очень большие числа за относительно короткое время. Сейчас на это требуется колоссальное количество времени и вычислительных ресурсов, и это лежит в основе работы алгоритмов открытого ключа. Значит, сразу после реализации квантового компьютера «посыпятся» все платежные карты (их можно будет вскрывать), соответствующие секретные шифры… Ясно, что к этому моменту человечество как-то подготовится и новую криптографию разработает, но квантовые компьютеры кардинально изменят мир. Это ответ на второй вопрос.

А на первый: теория хаоса — это достаточно модная вещь в последнее время. Но на самом деле теория хаоса возникла еще в работах Анри Пуанкаре (работа Пуанкаре была написана на приз короля Швеции Оскара II в 1890 году). Затем в 1918 году два французских математика — Гастон Жюлиа и Пьер Фату — написали работы по комплексной динамике на конкурс Парижской академии наук. Там впервые появились хаотические траектории, фракталы и множество Мандельброта. Потом эти результаты были забыты и тема снова возникла в работах украинского математика Александра Шарковского² в 1964 году. Одна из его работ была тогда опубликована, она очень интересная и проливает свет на чередование бифуркаций в нелинейных (квадратичных) системах с параметром. Почти в то же время появились работы американского метеоролога Эдварда Лоренца с его странным аттрактором, австралийского биолога Роберта Мэя с хаотическим поведением простейших моделей популяционной динамики и наконец «Период три означает хаос» (Period three implies chaos, 1975) американских математиков Джеймса Йорка (James A. Yorke) и Ли Тяньяня (Tien-Yien Li), где, собственно, и было предложено название этому направлению исследований: теория хаоса.

О чем говорит эта теория? Сначала вспомним, что такое детерминизм, детерминированная система. Это та, что зависит от предыдущего состояния однозначным образом, т. е. одинаковые причины вызывают одинаковые следствия. Но примеры из теории хаоса показывают, что даже в детерминированных системах и в очень простых системах типа квадратичных возможно поведение, которое полностью не предсказуемо. Оно как бы отчасти предсказуемо, потому что детерминировано, но по начальному состоянию траекторию вы в точности не сможете предсказать. Другими словами, траектория обладает всеми признаками стохастического процесса, т. е. ведет себя как монета, которая падает случайным образом. И тем не менее этот процесс детерминированный. Тут возникает вопрос: то, что мы видим как нечто случайное, не есть ли на самом деле такие же детерминированные процессы (а мы просто не знаем их поведения)? К этому имеет отношение так называемая чувствительная зависимость системы от начальных условий. Джеймс Максвелл об этом писал в популярной книге «Материя и движение» еще в 1888 году.

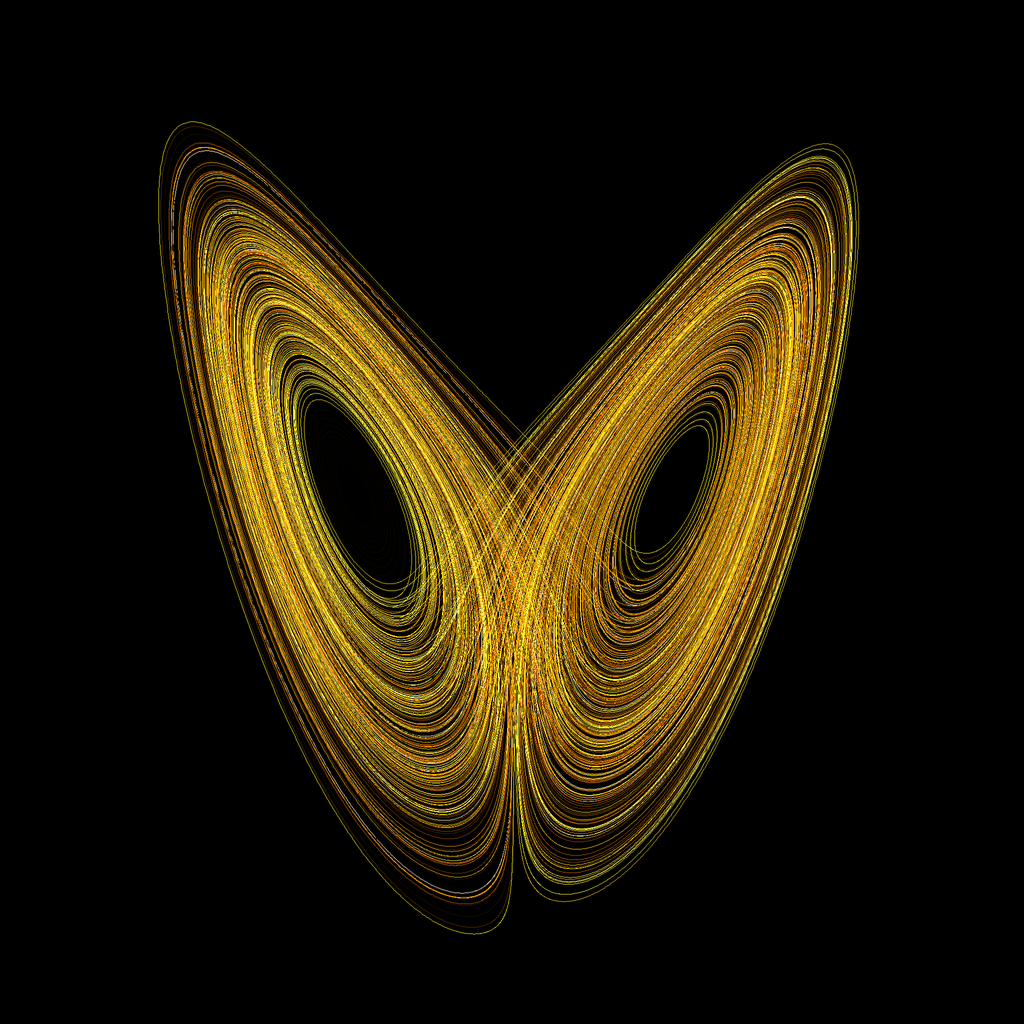
Речь идет вот о чем: маленькое изменение начальных условий приводит к сильному изменению следствий. Так называемый эффект бабочки. Этот термин достаточно популярен сейчас, есть даже фильмы с таким названием. Идея состоит в том, что, внося небольшие изменения, вы можете очень сильно изменить поведение системы. Вот это как раз имеет непосредственное отношение к теории хаоса. Такая вещь, например, как аттрактор Лоренца в метеорологии, описывает в некотором смысле «устойчивое» поведение какого-то атмосферного явления, но устойчивое в том смысле, что оно не уходит с некоторого аттрактора (множества притяжения), который является каким-то множеством в фазовом пространстве. Однако «фишка» в том, что небольшие изменения в начальных условиях резко меняют траекторию решения. Если говорить человеческим языком, то это означает, что какое-то небольшое изменение в каком-то месте атмосферы, ну, например, давления или еще какого-то параметра, типа температуры, может вызвать через достаточно непродолжительный срок в несколько недель сильные изменения погоды в каком-то месте. Буквально сильное или катастрофическое изменение: или будет ураган, или не будет урагана.

Как это связано с искусственным интеллектом? Безусловно, интересно предсказывать именно такие явления. Хотя сегодня, насколько я знаю, такой хорошей теории нет, как и хорошей архитектуры нейросетей тоже нет.

А почему это важно? Вот есть такая книжка Нассима Талеба «Черный лебедь. Под знаком непредсказуемости» (The Black Swan. To Impact of the Highly Improbable), где описан эффект появления «черных лебедей». Мы привыкли жить, скажем так, в эволюционирующей системе. Она развивается медленно и как-то плавно, но потом происходят какие-то революционные изменения, которые связаны с наличием явлений, которые мы не могли предсказать. Как правило, именно они наиболее интересны. Сама эволюция на малых участках в основном линейная, она малоинтересна, потому что это-то мы умеем предсказывать. Но вот почему, например, происходит резкое падение курса биткоина, крах экономики, война (еще можно привести массу событий, когда происходят резкие скачки в эволюции системы)? Этих вещей мы предсказать до сих пор не можем, насколько я знаю. Но в этом самое интересное и есть: создавать такие математические модели, такие архитектуры нейросетей, которые позволят предсказывать резкие изменения, незаметные в процессе эволюции системы, но обусловленные ее логикой. Образно говоря, распознавать, что система беременна кризисом.

— Что для вас случайность? Это действительно случайность или это что-то детерминированное, но что мы не умеем пока считать?

— Как писал Максвелл в упомянутой мной книжке, мы привыкли говорить, что одинаковые причины вызывают одинаковые следствия. Но одинаковых начальных условий в реальности нельзя добиться. Поэтому это нонсенс: эта максима не имеет смысла, поскольку ее посылка просто нереализуема. А вот другая максима, которая звучит по-другому, — «похожие причины вызывают похожие следствия» — это и есть в некотором смысле детерминизм. Во многих явлениях это действительно так, например в случае движения планет, а в некоторых — нет. Вот как раз там, где есть чувствительность к начальным условиям, там этого не происходит. Например, когда вы бросаете монетку, вам очень сложно бросить ее второй раз так, чтобы она ровно столько же оборотов совершила и упала той же самой стороной. То есть два раза повторить одинаково этот эксперимент не удастся, как бы вы ни старались, потому что это очень точная моторика должна быть у пальцев. Поэтому в этом явлении нет детерминизма — небольшое изменение начальных условий приводит к тому, что кардинально меняется результат: либо выпадает «решка», либо выпадает «орел».

Но ведь падение монетки может повлиять на что-то другое, это может быть выключатель какого-то устройства или перевод стрелок поезда — и поезд идет совершенно другим путем. Другими словами, там может быть усилитель, который вызывает иногда совершенно катастрофические изменения. Но теперь надо же как-то жить с этим. Можно сказать, что мы не знаем, как упадет монетка, но от этого пользы будет мало, если нас все-таки интересует, как в среднем она падает.

Скажем, нас может интересовать вопрос: сколько на 1000 бросаний монеток будет выпадений «орла»? Здесь мы уже можем использовать теорию вероятностей. В этом случае как раз работает закон больших чисел, который верен при некоторых предположениях, — что монетка правильная и всё такое (тут мы подходим как раз к основам теории вероятностей). Так вот, если все эти предположения имеют место, то мы можем достаточно точно на основании математических теорем сказать, что приблизительно будет. Например, при 1000 бросках монетки приблизительно 500 раз она выпадет «орлом». Причем мы можем сказать даже больше: что совершенно определенно ровно 500 не будет. То есть мы можем посчитать вероятность, что точно 500 «орлов» выпадет, но она достаточно маленькая. Порядка 0,025, т. е. меньше 3%. Мы можем сказать: не ставьте на это даже три доллара против ста — это, скорее всего, чрезвычайно редкое событие. А вот то, что это будет в районе 500 — между 400 и 600 — с очень высокой долей вероятности — это верно. И мы опять-таки можем сказать, с какой. Есть центральная предельная теорема, которая точно нам говорит, с какой долей вероятности это будет. Но что значит в повседневном смысле «вероятность»? Это значит, что вы можете ставить деньги в соответствии с этой теорией и выигрывать. Если вы играете в кости, то вряд ли будете ставить на 2. То есть если вы хотите выиграть при равных ставках, то, наверное, вы на 2 ставить не будете и на 12 не будете ставить, если вы бросаете две кости. Потому что понятно, что такая комбинация один раз только может выпасть, а ставить надо на 7, потому что такая сумма чаще всего выпадает. И если вы будете правильно считать вероятности, то, как правило, будете не проигрывать хотя бы, а может, даже и выигрывать, если ваш соперник неправильно считает. То есть это реально работает.

Это работает не только здесь, это и в квантовой механике работает, и везде работает — и в страховании работает, поэтому существуют страховые компании. Вероятностные законы достаточно адекватно описывают процессы, в которых есть статистика. Но говорить, что «с вероятностью 80% завтра будет дождь», для меня вот это нонсенс. Надо еще правильно понимать, что это значит. Я, к своему стыду, до сих пор не знаю, что такое «с вероятностью 80% будет дождь», хотя об этом всё время говорят синоптики. Это значит, что при таких метеоусловиях, как сегодня, в 80 случаях из 100 был дождь назавтра, или 80% времени будет идти дождь завтра, или что-то другое? Зачастую, когда приводят какие-то вероятностные оценки, люди просто не понимают, что за этим стоит. Или когда говорят «на 200% это верно» (что достаточно часто можно услышать), хотя вероятность всего 100%. Поэтому «правильная» вероятность вполне работает, она адекватно отражает мир. Отвечая на ваш вопрос: мне кажется, что вероятность связана с детерминированными процессами, но мы просто не знаем законов, по которым это происходит. Однако мы знаем другие законы — когда явление состоит из многих повторяющихся событий или это достаточно часто случается — там есть статистика. Пользуясь этими законами, мы можем достаточно точно предсказать, что будет происходить. Ну вот, скажем, газ: если слева в сосуде будет горячий газ, а справа — холодный, то температура будет выравниваться. Мы не знаем поведения молекул, мы не можем предсказать, куда одна конкретная молекула будет двигаться, но мы знаем статистические законы, и когда много этих молекул, то законы дают правильные выводы.

— Что происходит со случайными переменными в deep learning? Они не используются?

— Во-первых, они используются: для поиска правильных направлений, так скажем, этих весов, именно случайные переменные и используются. Очень интересный вопрос, где их брать? Когда Станислав Улам и Джон фон Нейман работали над проектом создания атомной бомбы в Америке, им нужно было смоделировать некую систему, где есть случайные переменные. Долгое время они не знали, что делать, поскольку пришлось бы изготавливать огромный сложный прибор, который моделировал бы всё это либо в физическом варианте, либо еще каким-то образом. Ну а потом Улам догадался, что эти случайные переменные, эту случайную последовательность можно просто генерировать такой последовательностью, как итерации функции 4x (1–x), просто подставляя вместо x число между нулем и единицей и делая соответствующие итерации. Оттуда в дальнейшем возник метод Монте-Карло. Тут мы начинаем практически с любого значения между 0 и 1 (скажем, 0,234523) и вычисляем значение этой функции f(x). Легко видеть, что при x на отрезке между 0 и 1 значение функции будет там же. Полученное значение снова подставляем в функцию. И так далее. Получаемая последовательность чисел на отрезке демонстрируют хаотическое поведение (по крайней мере статистически).

Детерминированная система, в данном случае квадратичная, генерирует случайную последовательность, что, в общем, довольно любопытно. Все сегодняшние алгоритмы, которые генерируют случайные числа, работают на этом принципе. Может быть, они устроены более изощренно, но принцип один и тот же. Выбирается или конструируется какая-то детерминированная система, у которой так называемое хаотическое поведение. Значения, которые она выдает, — например, числа от нуля до единицы — обладают всеми признаками случайной величины. Они появляются не в одном месте, скажем, не все они меньше ½ — как-то равномерно распределены между нулем и единицей.

Я вам больше скажу: возьмите число π, которое равно отношению длины окружности к диаметру, — это число хорошо известно, и его десятичные знаки после запятой найдены, наверное, до 10³⁰ цифр или даже больше (на июнь 2022 года известны первые 100 трлн знаков числа π после запятой. — Прим. ред.) — так вот давайте это число представим в двоичном коде, тогда π будет выглядеть как цепочка нулей и единиц (11,00100100001111110110. — Прим. ред.). Известно, что это число иррациональное, более того, трансцендентное, и поэтому оно никогда не прекращается. Эта последовательность нулей и единиц не может ни прекратиться, ни периодически повторяться. Это и есть признак иррациональности этого числа. А теперь давайте бросим монету и станем смотреть и записывать: когда выпадает «орел» — будет нолик, «решка» — единичка; посмотрим на эти нули и единички. Так вот: если мы будем смотреть на эти две последовательности, то они почти одинаковые. Не в том смысле, что точно повторяются, — просто у них одинаковое статистическое поведение. Скажем, в среднем нулей будет примерно половина в разложении числа π на больших интервалах. Все вероятностные законы, которые, насколько мне известно, существуют в теории вероятностей и касаются «честной монетки», — все эти статистические законы при разложении числа π в двоичную дробь выполняются. Поэтому, если вы хотите взять какое-то случайное число, то, например, вы можете взять какой-то кусок двоичного разложения π. Получится двоичное число, и вот вы переведете его в десятичное и получите псевдослучайное. По крайней мере, очень маловероятно, что кто-то его угадает, несмотря на то, что π самое что ни на есть детерминированное число. Оно же конкретное число и его можно вычислить массой способов, и всегда знаки одни и те же, они же не случайным образом возникают! Вы просто берете какой-то ряд — и в этом ряду берете всё больше и больше цифр у π, у вас возникает слагаемое за слагаемым, цифра за цифрой. Есть масса разных алгоритмов и способов вычислений. Детерминированный процесс выдает «случайное» поведение почему-то.

Хотя, опять же, хочу оговориться, что это одна из нерешенных математических задач. Многим кажется, что в математике уже всё известно. Однако это не так. Вот это, например, открытая и действительно интересная математическая проблема. Правда ли, что в среднем число нулей в двоичном представлении π такое же, как число единиц? То есть если мы возьмем большой кусок представления числа π в двоичной системе и посчитаем там число единиц, поделив его на длину этого куска, то будет ли всё это стремиться к ½, если мы будем увеличивать и увеличивать тот отрезок, который рассматривается? Неизвестно. Это открытая математическая проблема, и до сих пор никакого продвижения здесь нет, но все считают, что это именно так.

— Над чем вы сейчас работаете?

— Сейчас я в основном занимаюсь скорее изучением deep learning и всего, что с этим связано. Есть идея, о которой я сейчас не хочу говорить, потому что она очень сырая, но она позволяет создать определенный стартап. Если же говорить о том, что меня интересует с научной точки зрения, то это вот что… Раньше я занимался вопросами стабилизации динамических систем, а сейчас мне интереснее то, о чем мы сегодня говорили: каким образом эти «черные лебеди» могут быть предсказаны. Вы наблюдаете какой-то процесс, который, грубо говоря, стабилен, не демонстрирует никаких признаков перехода к катастрофическому сценарию, т. е. процесс достаточно «хороший», гладкий, он развивается предсказуемо. Однако где-то там, внутри логики этого процесса, уже заложены механизмы будущей катастрофы, его переход в какое-то резко меняющееся состояние.

Можно привести очень простой пример системы с таким поведением. Пусть каждое последующее число равно сумме двух предыдущих. Это широко известный пример — последовательность Фибоначчи. Она начинается с двух единиц. Но мы можем начать не с единичек, а с других чисел. Например, взять –1 и 0,6180339… Второе число — это золотое сечение. Начинаем с чисел –1 (минус один) и этого второго, берем их сумму. Получаем –0,381966. Дальше берем сумму последних двух (0,6180339 и –0,381966). Еще ближе к 0. Так повторяем 30 шагов. Выйдем на 0 с точностью до 7 знака. Но где-то на 40–50-м шаге оторвемся и уйдем на бесконечность (следуя лишь внутренней логике системы). График поведения такой системы — этакий синусоидальный, затухающий, — синусоидально-затухающая волна. Настолько затухающая, что будет 0 в седьмом знаке на 30-м шаге, а на графике будет 0. Но вот этот ноль вдруг через какое-то время начинает расти по этому же закону (каждое следующее число равняется сумме двух предыдущих) — и вдруг выходит на катастрофические показатели роста. На 60–70-м шаге уже выходит за размеры Вселенной, если в числовом выражении. Я понимаю, что это самый простейший модельный пример, и объяснение легко дать, зная закон динамики. Но как определить по поведению системы, не зная динамики, что там внутри? Как узнать, что система «беременна» кризисом? Это интересная и важная, можно сказать, центральная проблема. Ведь если бы мы знали в экономике, что скоро будет кризис по каким-то данным, мы бы могли его смягчить. Или, исследуя человека, по его температуре, давлению, анализам крови смогли бы сказать, что велика вероятность скорого инсульта. Это амбициозная задача, и какое-то продвижение в ней будет, как мне кажется, весьма интересно.

— А в чем цель deep learning? Что мы делаем? Это познание мира, подчинение, прогнозирование? Где та точка, в которую мы хотим прийти?

— Более интересный вопрос не в том, какова цель, а куда мы придем. Люди, которые создавали первые компьютеры, полагали, что те будут использоваться в основном для научных вычислений, будут помогать считать ученым, делать серьезные математические расчеты. Что за этими компьютерами будут сидеть серьезные бородатые дяди, двигающие вперед науку, а всё человечество — к светлому будущему. Но на самом деле компьютеры сейчас используются в основном для развлечений, а через Всемирную сеть, созданную для обмена научными данными, качают порнуху. И если вы спросите среднестатистического человека, зачем ему компьютер (хотя компьютер ему сейчас, может, уже и не так нужен, достаточно смартфона), то окажется, что нужен он в основном для того, чтобы зависать в социальных сетях, для коммуникации, для того, чтобы заглянуть в Google Map, чтобы знать, как проехать на машине…

К чему я это говорю? Создание компьютеров подразумевало совсем иную цель, используются они вовсе «не по назначению». Так вот, я думаю, что то же самое будет и с искусственным интеллектом. Я не берусь тут строить прогнозы, где именно он будет использоваться. Возможно, для создания компаньонов одиноким людям или чтобы менять свои сетевые образы, как сейчас делает Lensa. В ней тоже используются элементы искусственного интеллекта. Но для чего? Не для новых открытий, а для entertainment…

Был такой писатель Владимир Савченко, еще советский. Он написал роман «Открытие себя». Там есть такая фраза: «Если коровы когда-нибудь в процессе своей естественной эволюции научатся читать, они тоже начнут именно с детективов и любовных историй». Я не хочу сравнивать человечество с коровами, но факт остается фактом. Ведь даже о себе самом я могу сказать то же самое. Так что неважно, что ученые намеревались применять искусственный интеллект для того, чтобы решать какие-то свои научные задачи, — скорее всего, когда-нибудь он будет использоваться прежде всего в быту для избавления от каких-то рутинных задач и наверняка позволит покончить с какими-то профессиями, которые до сих пор не могли обойтись без человека.

Для меня ИИ интересен тем, что он может быть подспорьем для какого-нибудь математического творчества. Этот вопрос очень серьезно обсуждался недавно в математическом сообществе: сможет ли машина заменить математика? То есть сможет ли машина, например, решить вопрос с гипотезой Римана или аналогичные какие-то проблемы? Это уже намечается в первом приближении. Задача четырех красок решена компьютером, но пока еще алгоритмы пишут люди. А вот сможет ли машина с нуля всё это сделать?

На самом деле, исходя из того, что машины сегодня обыгрывают людей-чемпионов в шахматы и в го, это всё уже, наверное, не за горами. Но мне кажется, что даже не сам искусственный интеллект интересен, а создание новых компьютеров, которые быстро считают и считают принципиально по-другому, — квантовых компьютеров. И если они будут созданы и соединятся с deep leaning, то там сложно уже будет сказать, как дальше пойдет развитие человечества. Я не Герберт Уэллс, боюсь предсказывать, тем более, что предсказания, как правило, не работают. Единственное предсказание, которое до сих пор всегда сбывалось, — это то, что ни одно предсказание не будет верным.

— Когда мы это всё сделаем, как оно на нас повлияет?

— Хотелось бы, чтобы мало. Я и сейчас чувствую уже сильную вовлеченность в социальные сети, в эту современную, далекую еще от искусственного интеллекта среду, в которой мы теперь живем. И это уже напрягает, я думаю, не только меня. Но я боюсь что-то прогнозировать, хотя можно спрогнозировать и восстание машин, и порабощение человечества, и вообще уничтожение всех людей как ненужной уже стадии эволюционного процесса. То есть, поскольку искусственный интеллект создан, промежуточная стадия уже не нужна. Ну а может они человечество и сохранят как исчезающий вид…

Если один человек может привести мир к состоянию, близкому к термоядерной войне, то почему этого не может искусственный интеллект? Тоже может. Мы должны как-то поменять систему, чтобы не было возможности такого централизованного управления, потому что централизованное управление приводит как раз к нестабильности системы. Это известные факты, никаких открытий я не делаю.

В основе этого очень простая математика: если у вас есть цепочка дифференциальных уравнений, где каждое зависит от предыдущего, то соответствующая линейная часть будет иметь характеристический многочлен с комплексными корнями, распределенными по окружности. Ну, я сейчас мудреные слова говорю, но на самом деле там сразу появляются корни, которые лежат в правой полуплоскости и ответственны за дисбаланс системы. Другими словами, это некоторая такая математическая теорема, утверждающая, что если у вас есть централизованное управление, то оно обязательно приведет к катастрофе. И задача стоит в том, чтобы это как-то распределить, размыть это управление, создать более размытую структуру.

Если аналогию приводить, то кусок скалы — он, конечно, несокрушимый и твердый, Но кусок скалы иногда падает и распадается на куски, при этом ломая всё на своем пути. Как и сам камень, он неустойчив, он может упасть в любую сторону, особенно если его на острие поставить. Ну а песок очень устойчив, на песке вы можете спокойно стоять: он сыпуч, гибок и мягок. Поэтому союз городов-полисов в Греции был гораздо более устойчивым, чем империи типа Персидской. Но это уже другая тема.

¹ odessa-life.od.ua/article/society/odessity-za-granicej-zhizn-pod-parusom-aleksej-soljanik-devjat-let-zhivet-na-trimarane

² un-sci.com/ru/2020/11/29/intervyu-so-vsemirno-izvestnym-matematikom-a-n-sharkovskim-iz-kieva/