
Известность Марине Вязовской принесли ее работы по решению задачи об упаковке шаров в высоких размерностях. В этой задаче ставится вопрос, каков плотнейший способ упаковки единичных неперекрывающихся сфер (или шаров) в евклидовом пространстве. В пространстве размерности 1 мы можем полностью покрыть всю прямую. На плоскости (n = 2) в 1773 году Лагранжем было показано, что гексагональная упаковка наиболее плотна. В 1611 году Кеплер выдвинул печально известную гипотезу, что в пространстве плотнейшими упаковками являются кубическая плотная упаковка и гексагональная плотная упаковка (плотность у них одинаковая). И в 1998 году эта гипотеза была доказана Томасом Хейлсом с привлечением больших компьютерных вычислений.
Итак, до недавнего времени эта задача была полностью решена только для размерностей 1, 2 и 3. Однако в 2016 году Марина Вязовская сделала поразительный прорыв, решив проблему плотнейшей упаковки для восьмимерного пространства, показав, что исключительно симметричная упаковка (известная как корневая решетка группы E8) является наиболее плотной. И менее чем через неделю после этого Вязовская вместе с Генри Коном, Абхинавом Кумаром, Стефаном Миллером и Данило Радченко решила эту же задачу для 24-мерного пространства. Ими было показано, что замечательная решетка Лича является наиболее плотной упаковкой.
Эти два измерения, 8 и 24, были давно известны как особенные, благодаря существованию исключительно симметричных решетчатых упаковок. В 2003 году Генри Кон и Ноам Элкис (опираясь на работы Дельсарта) предложили использовать методы линейного программирования для продвижения в решении задачи упаковки сфер, что в принципе могло решить задачу о плотнейшей упаковке шаров в пространствах этих двух размерностей. Однако для продвижения по этому пути они нуждались в существовании «магической функции» с замечательными Фурье-аналитическими свойствами.
Несмотря на убедительные численные свидетельства, что такая магическая функция существует, они были неспособны построить такую функцию. Искусно используя свойства (квази)модулярных форм, Вязовская смогла построить требуемые магические функции и проверить их свойства, завершив решение задачи упаковки шаров для этих двух размерностей. Затем Марина адаптировала эти конструкции для получения дальнейших результатов в анализе Фурье, связанных с принципом неопределенности и формулой суммирования Пуассона.
Теренс Тао, лауреат премии Филдса,
профессор математики в Калифорнийском университете в Лос-Анджелесе (США)
Плотные упаковки шаров
Михаил Цфасман, гл. науч. сотр. ИППИ РАН, directeur de recherches au CNRS, проректор Независимого московского университета:
Шар — это множество точек, отстоящих от центра на расстояние, не превосходящее радиуса. На прямой этому же определению удовлетворяет отрезок, на плоскости — круг.
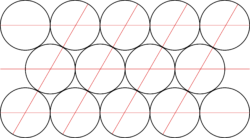
Как плотно уложить равные отрезки на прямой? Очевидно, кладем отрезки встык — они покрыли всю прямую. А круги на плоскости? Тоже понятно: кладем круги по одной линии, скажем горизонтальной, потом выше и ниже кладем круги в параллельную линию, но сдвигая их так, чтобы эта линия была возможно ближе к первоначальной, и так далее. Просто и всем ясно, что плотнее нельзя. А как это доказать? Вы будете смеяться, но доказательство было получено только в середине XX века (Ласло Фейеш Тот, 1940), и оно весьма непросто.
Если разрешать укладывать круги только очень регулярным образом, так, чтобы центр одного из кругов был в начале координат, а сумма и разность центров кругов была также центром (такие упаковки называются решетчатыми, или просто решетками), то задача сильно упрощается, ее решил еще в XVIII веке Жозеф Луи Лагранж.
А как укладывать равные шары в трехмерном пространстве? Известного английского поэта, адмирала и пирата, закончившего свою жизнь на эшафоте, сэра Уолтера Рэли этот вопрос интересовал с точки зрения укладки пушечных ядер на корабле. Он задал его своему советнику по науке, одному из лучших ученых того времени Томасу Хэрриоту, который записал свои размышления по этому поводу в письме к Иоганну Кеплеру. Тот опубликовал этот вопрос в своей книге про форму снежинок — с тех пор эта проблема называется задачей Кеплера.
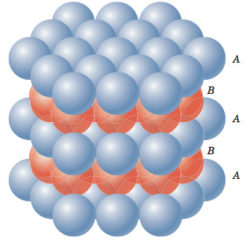
Положим шары на стол так, чтобы их проекции на стол образовывали плотнейшую упаковку кругов, и склеим шары между собой. Возьмем второй экземпляр такого же слоя шаров, приподнимем его и положим сверху так, чтобы он был возможно ниже, т. е. так, чтобы шары второго слоя легли в углубления первого. Потом третий слой, и так далее. Получим упаковку всего пространства, в ней каждый шар касается шести других. Так торговцы фруктами укладывают апельсины на прилавке. Опять же, очевидно, что лучше нельзя. То, что более плотных решеток не бывает, доказал Карл Фридрих Гаусс, а вот то, что никаких более плотных упаковок не бывает, доказал Томас Хейлс в самом конце XX века. Мало того что доказательство очень длинное, сложное и непрозрачное, оно еще и использует большие компьютерные вычисления.
А в четырехмерном пространстве? Можно перейти от трехмерного к четырехмерному так же, как мы переходили от плоскости к трехмерному пространству. Будет ли эта упаковка плотнейшей? Среди решеток — да, а среди всех упаковок — этого мы не знаем и вряд ли будем в ближайшее время знать.
В высоких размерностях метод слоев работает плохо, но до размерности 8 им можно пользоваться, применяя различные дополнительные хитрости.
До размерности 8 включительно и, неожиданно, в размерности 24 мы знаем плотнейшие решетчатые упаковки. Почему именно для 8 и 24? Оказывается, что именно в этих размерностях кандидаты в плотнейшие упаковки имеют необыкновенно много симметрий. Для общей задачи Генри Кон и Ноам Элкис придумали изящный вариант метода линейного программирования, позволивший доказать, что наибольшая возможная плотность очень близка к плотности известных нам упаковок. Особенно хорошее приближение у них получается в размерностях 8 и 24, так как там наилучшие решетки обладают огромным количеством симметрий. Так, для 24 порядок разницы не превышает 10-30. Этот метод требует аккуратного выбора так называемой тест-функции. Тест-функции можно улучшать, хоть это и очень непросто. А можно ли выбрать такую тест-функцию, чтобы она решила нашу задачу точно?
С этой задачей в 2016 прекрасно справилась Марина Вязовская. Будучи ученицей Дона Цагира, она занималась теорией модулярных форм — функций, которые хорошо себя ведут при преобразовании группами симметрий плоскости Лобачевского. Именно среди комбинаций модулярных форм ей удалось найти оптимальные тест-функции, полностью решающие задачу, сперва для размерности 8, а затем (в соавторстве с Коном, Кумаром, Миллером и Радченко) и в размерности 24. Блестящее и неожиданное достижение!
Для размерностей от 4 до 7, от 9 до 23 и больше 25 проблема до сих пор открыта и, видимо, очень трудна.
А что делать для совсем больших размерностей? Здесь приходится быть много скромнее. Не надеясь на обнаружение плотнейшей упаковки шаров, мы просто ищем достаточно плотные упаковки; каждый новый рекорд — уже победа. Автор этих строк предложил использовать для построения плотных упаковок в очень высокомерных пространствах конструкции из алгебраической теории чисел и алгебраической геометрии над конечным полем. Получаются хорошие упаковки, но хотелось бы еще лучше. Поиск продолжается.
В заключение заметим, что эта красивая математическая задача полезна не только для укладывания пушечных ядер и апельсинов. Она тесно связана с геометрией, алгеброй, теорией чисел и даже с теорией передачи и хранения информации.
«Мои любимые задачи — об оптимальных конфигурациях в метрических пространствах»

Марина Вязовская, выпускница Киевского университета, профессор Федеральной политехнической школы в Лозанне (Швейцария), ответила на несколько вопросов нашей газеты.
— Как вы решили прийти в математику? Были ли сомнения в выборе?
— Мой путь в математику был довольно обычным и неинтересным. Математика была моим любимым предметом начиная с младших классов. Мне нравилась строгость и простота математических законов, позволяющих самостоятельно находить ответы на сложные и неочевидные вопросы. В старших классах я перешла из обычной школы в физико-математический лицей. Атмосфера физмат-школы, дух соревнования и огромная поддержка учителей сделали мое решение дальше изучать математику простым и естественным.
Сомнения в том, какую профессию выбрать, возникли в конце четвертого курса, когда пришло время искать работу. Но как раз в это время я получила свой первый научный результат и увидела, что доказывать собственные теоремы намного интереснее, чем изучать уже готовые теории или решать искусственно придуманные олимпиадные задачи. Я поняла, что ни в какой другой профессии мне не будет так интересно.
— Как бы вы описали область ваших математических интересов?
— Я занимаюсь теорией чисел. Теория чисел нравится мне тем, что очень трудно придумать математическую задачу, которая не была бы с ней связана. Мы не знаем, какие методы понадобятся математикам, чтобы решить гипотезу Римана, Бёрча — Свиннертон-Дайера или АВС-гипотезу. Конечно, нельзя объять необъятное, и мои любимые задачи — это задачи об оптимальных конфигурациях в метрических пространствах.
— Не могли бы вы в научно-популярном формате (нас читают не только физики, но и филологи) описать тот результат, который был отмечен премией Европейского математического общества?
— Мне присудили премию за решение одной из таких задач — задачи о плотнейшей упаковке шаров в пространствах размерности 8 и 24. В этой задаче ставится вопрос, какое наибольшее количество шаров радиуса 1 может уместиться в большой (очень широкой, длинной и высокой) коробке. Если все размеры коробки достаточно велики по сравнению с шарами, то это количество будет в основном зависеть от объема коробки и мало зависеть от ее формы, а отношение максимального количества шаров к объему будет стремиться к некоторому постоянному числу, оптимальной плотности.
Задача об оптимальной упаковке в размерности 3, известная как задача Кеплера, была решена в 1998 году Томасом Хейлсом. И такая история очень типична в теории чисел, когда «безобидный» и даже наивный вопрос ждет своего решения несколько столетий. Оптимальные конфигурации, достигающие максимальной плотности, были известны Кеплеру и его современникам, но математическое доказательство их оптимальности стало возможно лишь в наше время благодаря развитию теоретических знаний и вычислительной техники.
Мне удалось решить аналогичную задачу в размерностях 8 и 24. В этом случае оптимальные конфигурации тоже были известны, и весь «фокус» был в том, чтобы доказать оптимальность.
people.epfl.ch/maryna.viazovska






Представить себе сейчас не могу практического применения работ по многомерным (4+) пространствам, но похоже на работу того средневекового монаха, что придумал мнимую величину j — уж ей-то мы пользуемся вовсю!
Любая теплотехническая система (отопление или охлаждение, например) описывается минимум 5 переменными: временем, плотностью теплоносителя, давлением, температурой, энтальпией. А упаковка шаров — это из теории кодирования задача, где размерность — это количество бит в слове. Шар с центром в каком-то слове здесь — это сам код и множество всех слов с ошибкой в не более чем в r битах. Надо подобрать все кодовые слова так, чтобы эти шары не пересекались и при этом чтобы сами слова были не слишком длинные.
можно было еще упомянуть про спор Ньютона и Грегори о проблеме «13-го поцелуя» — сколькими шарами можно окружить один шар — 12-тью или 13-тью. Из этой проблемы видна важность симметрии при оценке плотности упаковки, т.к. центросимметричный икосаэдр чуть-чуть, но плотнее, чем ГЦК и ГПУ структуры.