
Премия Дирака за 2016 год присуждена Аркадию Вайнштейну, Михаилу Шифману из Института теоретической физики имени Файна в Университете штата Миннесота и Натану Зайбергу (Nathan Seiberg) из Института передовых исследований Принстонского университета. Высокой наградой отмечены выдающиеся результаты в квантовой хромодинамике вне рамок теории возмущений и точные результаты в суперсимметричных теориях («to a better understanding of field theories in the non-perturbative regime and in particular for exact results in supersymmetric field theories»). Премия, безусловно, заслуженная.

Что стоит за этими сухими формулировками? Главное действующее лицо в этой пьесе — вакуум квантовой хромодинамики (далее КХД) — теории сильных взаимодействий, сформулированной в современном виде в 1973 году Марри Гелл-Манном, Генрихом Лейтвилером и Харальдом Фритчем. Прошло уже больше 40 лет, а как устроен вакуум КХД — основное состояние системы, так доподлинно и неизвестно.
Произносится стандартное заклинание: «Вакуум КХД — дуальный сверхпроводник», но то, что понимание очень приблизительное, да и не полученное до сих пор из первых принципов квантовой теории поля, ясно всем. Вопрос про вакуум КХД, или, иными словами, проблема конфайнмента (удержания кварков), по праву входит в тройку наиболее важных проблем фундаментальной физики, вместе с вопросом о квантовой гравитации и природе темной энергии и темной материи.
Итак, вакуум КХД. Мы точно знаем, что КХД — асимптотически свободная теория; то есть элементарные частицы КХД — глюоны и кварки слабо взаимодействуют между собой на малых расстояниях и сильно взаимодействуют на больших. Слова «большие» и «малые» читатель должен принимать с осторожностью: и то и другое относится к очень малым расстояниям с макроскопической точки зрения, а теория сама задает масштаб, относительно которого мы и отсчитываем величины.
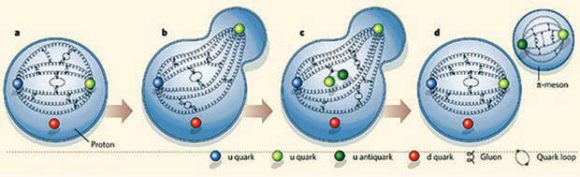
Из-за того что сила взаимодействия увеличивается с расстоянием, между кварками протягивается струна, которая не дает кваркам существовать независимо, — в этом и состоит явление конфайнмента (от англ. confnement — удержание, ограничение. — Ред.). Как возникает струна КХД и какое свойство вакуума КХД ответственно за ее возникновение — вопрос исключительно сложный. Замечу, что именно попытки удовлетворительного описания рассеяния частиц в теории сильных взаимодействий и привели к созданию теории струн в конце 1960-х — начале 1970-х годов.
Физикам интересны различные свойства частиц — мезонов и барионов, их распадов и превращений. Можно ли их вычислить сколько-нибудь самосогласованным образом? Если поставить такую задачу, то нужно учитывать, что, как любой квантовый объект, вакуум КХД представляет из себя сильно флуктуирующую среду, виртуальные возбуждения рождаются и умирают в нем постоянно. Причем ситуация с вакуумом КХД осложняется тем, что в нем есть два типа вакуумных флуктуаций, которые для простоты мы назовем малыми и большими.
Для наглядности стоит представлять себе маятник на подвесе. Для него малые флуктуации — небольшие колебания маятника относительно положения равновесия, а большие — когда маятник совершает полный оборот вокруг точки подвеса.
Конечно, второй процесс классически невозможен, если только маятник очень сильно не толкнуть, но мы уже оказались в квантовом мире, в котором возможно всё, только с разной вероятностью. Про большие флуктуации можно сказать, что они возникают как результат квантового туннелирования и имеют нетривиальные топологические свойства. В физике они называются инстантонами, но мы постараемся не использовать этот термин без необходимости. Другое их название — непертурбативные флуктуации. Впервые в квантовой теории поля они были найдены в 1975 году в знаменитой работе А. Белавина, А. Полякова, А. Тюпкина и А. Шварца.
Внимательный читатель наверняка уже понял, что учет всех флуктуаций, больших и малых, которые еще и крайне сложно взаимодействуют друг с другом, выглядит безнадежной задачей. Но тут на помощь приходит союз глубокой физической интуиции и строгих математических аргументов.
Важность такого союза прекрасно понимают все три лауреата премии. В конце 1970-х в серии работ Аркадия Вайнштейна, Валентина Захарова и Михаила Шифмана были сформулированы правила сумм ВЗШ, которые оказались исключительно эффективны для вычисления физических характеристик сильновзаимодействующих частиц.
Каким образом удалось решить вопрос суммирования по всем типам вакуумных флуктуаций, большим и малым? С помощью изящных математических аргументов получилось сформулировать два разных представления для разных величин, не вычисляя бесконечные ряды по флуктуациям с неизвестными коэффициентами. Сравнивая два представления, оказалось возможным вычислять характеристики частиц и сформулировать правила сумм.
Но каким образом удалось учесть исключительно сложную структуру вакуума КХД? Сложность основного состояния было предложено зашифровать набором так называемых вакуумных конденсатов, чьи значения — мировые постоянные. Но ведь конденсатов тоже бесконечно много, поэтому на первый взгляд мы просто переписали одну нерешаемую задачу через другую.
Однако оказалось, что можно сформулировать правила сумм так, что только два вакуумных конденсата — киральный и глюонный — будут играть ключевую роль. Эти конденсаты говорят, что в вакууме КХД нарушена лево-правая симметрия и симметрия относительно изменения масштаба. И если киральный конденсат был известен ранее, то глюонный конденсат был введен и найден из сравнения с экспериментом именно в этих работах.
Детали того, каким образом он возникает из суммирования по большим флуктуациям вакуума КХД, до сих пор неизвестны, но его значение с достаточно хорошей точностью определено. Глюонный конденсат дает вклад в темную энергию, причем его вклад намного превышает значение, известное из космологических данных. Каким образом этот вклад сокращается — открытый вопрос.
Одно из основных увлечений теоретиков — поиск новых симметрий, а после того как симметрия обнаружена, немедленно столь же увлеченно ищется механизм ее нарушения. Так произошло и с суперсимметрией, предложенной в 1971 году в ФИАН Юрием Гольфандом и Евгением Лихтманом. В рамках суперсимметрии объединяются «коллективисты» бозоны и «индивидуалисты» фермионы. Синтез суперсимметрии и КХД привел к созданию суперсимметричной квантовой хромодинамики — нашему следующему персонажу.
Скептик, разумеется, скажет, что суперсимметрия в природе не найдена и является всего лишь теоретической игрушкой. Не будем спорить и пока воспримем суперсимметричную КХД как интересную модель. Зададим такой же вопрос: как устроен вакуум суперсимметричной КХД и как устроены малые и большие флуктуации на его фоне? Во-первых, можно строго показать, что вакуум не один — их несколько. Во-вторых, в силу дополнительной симметрии происходят некоторые сокращения нежелательных эффектов и возникает надежда, что про вакуум в такой среде можно сказать несколько больше, чем в теории без супер-симметрии.
В 1982–1984 годах в серии работ, выполненных в ИТЭФ, изучались и стантоны в суперсимметричной КХД — большие флуктуации в вакууме. Были обнаружены два новых красивых и неожиданных явления, оказавших большое влияние на дальнейшее развитие квантовой теории поля.
Во-первых, оказалось, что малые флуктуации на фоне большой (мелкое дрожание маятника при полном обороте вокруг точки подвеса) знают про то, как ведет себя константа взаимодействия теории при разных масштабах, — была найдена так называемая ВЗНШ (Вайнштейн — Захаров — Новиков — Шифман) точная бета-функция. Это был, по-видимому, первый пример, когда в квантовой теории поля без дополнительных законов сохранения удалось точно учесть вклад всех малых флуктуаций в некоторой физически важной величине.
Во-вторых, оказалось, что возникает необычная ситуация, когда два пробных объекта, вставленных в разные точки пространства, не знают про расстояние между этими точками. Это позволило вычислить один из вакуумных конденсатов в теории.
Оба результата оказались глубокими, и их важность была оценена не сразу. Первый — о скрытой структуре во взаимосвязи малых и больших флуктуаций (пертурбативных и непертурбативных) — только сейчас начинает приобретать относительно стройный вид; второй оказался первым примером «топологических корреляторов» в нетопологической теории поля.
Топологические квантовые теории поля, в которых отсутствует понятие расстояния, были строго сформулированы только в конце 1980-х годов в работах Альберта Шварца (Albert Schwarz) и Эдварда Виттена (Edward Witten) и оказали очень серьезное влияние на математику и ее тесную связь с квантовой теорией поля.

Чем знаменит третий лауреат? В 1993–1994 годах появились работы Натана Зайберга, где было сформулировано то, что сейчас называется дуальностью Зайберга. Была высказана гипотеза, что есть крайне нетривиальные связи между разными суперсимметричными теориями поля.
Объяснить суть этой гипотезы непрофессионалу довольно трудно, поэтому ограничимся тем, что попробуем пояснить, почему она так важна. Как мы уже много раз говорили, есть малые и большие флуктуации вакуума. Режим, когда доминируют малые флуктуации, называется режимом слабой связи; когда большие — режимом сильной связи. Понятно, что в режиме слабой связи, когда эффекты взаимодействия невелики, вычисления проводить проще.
Так вот, дуальность Зайберга связывает две теории, одна из которых находится в режиме сильной связи, а вторая — в режиме слабой связи. Это позволяет получать интересные результаты в теории с сильной связью таким образом: используем преобразование дуальности и переводим ее в режим слабой связи в другой теории, проводим там относительно простые вычисления и транслируем результаты этих вычислений назад в исходную теорию. Наверное, так же актер, сыгравший роль в новом для себя амплуа, узнает о себе самом что-то новое.
Такой трюк позволяет делать интересные предсказания. Например, элементарные частицы в одной теории могут оказаться составными в другой. Математически строгого доказательства дуальности Зайберга нет до сих пор, но она оказалась очень полезна для прояснения физической картины. Эти работы вызвали волну интереса к понятию дуальности в достаточно широком контексте, и сейчас число теорий, связанных друг с другом той или иной дуальностью, велико.
Более того, оказалось, что и разные версии теории струн связаны между собой преобразованиями дуальности, что позволило объединить все версии теории суперструн в одну М-теорию — теорию мембраны в 11-мерном пространстве.
Можно ли точно учесть все большие вакуумные флуктуации? В 1994 году появились две работы Зайберга и Виттена, в которых в расширенной суперсимметричной квантовой хромодинамике (не спрашивайте, что это такое) был найден точный ответ для ряда физически важных величин, включая спектр масс стабильных частиц. В силу того что в теории с расширенной суперсимметрией малые вакуумные флуктуации учесть относительно легко, основная проблема свелась к учету больших флуктуаций.
Эти работы до сих пор производят сильное впечатление, авторам удалось пройти по самой грани между исключительной физической интуицией и тем, когда начинается не очень мотивированный полет фантазии. На этой грани их удержали используемые довольно тонкие математические результаты и аргументы.
В итоге с помощью магических заклинаний, в которых упоминались дуальность, голоморфность и ренормализационная группа, «из шляпы достали кролика» и, не проводя явных вычислений вкладов больших флуктуаций, «угадали» точный ответ, выдержавший все простые проверки.
В этот момент показалось, что проблема конфайнмента в КХД вот-вот будет решена. Однако радость оказалась преждевременной. Для того чтобы объяснить конфайнмент в обычной КХД, нужно было сначала теорию с расширенной суперсимметрией нарушить до теории с простой суперсимметрией, а на втором шаге нарушить теорию с простой суперсимметрией до КХД, где суперсимметрии нет совсем.
Первый шаг был быстро сделан, и было показано, что действительно за счет суммирования больших флуктуаций возникает конденсат монополей — механизм конфайнмента, ожидаемый в КХД. Но сделать второй шаг оказалось очень сложно, исследования в этом направлении продолжаются до настоящего момента.
Потребовалось почти десять лет, чтобы получить «угаданный» результат Зайберга — Виттена из первых принципов прямым суммированием всех больших вакуумных флуктуаций. Это удалось сделать только в 2002 году Никите Некрасову с помощью красивого трюка.
Оказалось, что удобно закрутить весь наш четырехмерный мир (три координаты + время) с небольшой угловой скоростью. Позволим себе несколько рискованную аналогию. В центрифуге мы можем пытаться отделить те «вклады», которые нас интересуют, — нечто похожее было сделано Некрасовым, и результат полного суммирования больших вакуумных флуктуаций «в центрифуге» сейчас носит название статистической суммы Некрасова. Результат Зайберга — Виттена был полностью подтвержден.
Дуальность Зайберга и решение Зайберга — Виттена оказались тесно связаны с геометрией 11-мерного пространства и картиной «мира на бране». Читатель должен постепенно привыкать к мысли, что он живет на шестимерной поверхности («бране»), вложенной в 11-мерное пространство. Это должно его порадовать, или он должен с этим смириться, всё зависит от темперамента.
Дуальность Зайберга оказалась просто движением бран в многомерном пространстве, а результат точного суммирования больших флуктуаций вокруг вакуумного состояния оказался эквивалентен тому, что форма «нашей браны» принимаеточень конкретный вид. Именно форма браны и определяет набор стабильных частиц и их массы.
Конечно, наука — это игра с Богом в прятки, где ты всегда играешь роль водящего. Но выбор, какой же объект мы будем искать, в наших руках, и надо отдать должное лауреатам, они выбрали в высшей степени достойные для поиска цели. Мне, конечно, проще писать об Аркадии и Мише, они до 1990 года работали в России и были одними из главных действующих лиц в золотые десятилетия ИТЭФ, в 1970-е и 1980-е годы, когда он, безусловно, был в пятерке ведущих мировых центров по теоретической физике. Они играли важную роль в создании совершенно уникальной научной атмосферы тех лет.
Когда Аркадий приезжал в ИТЭФ из Новосибирска, а это бывало очень часто, работа начиналась утром, а вечером, когда все расходились по домам, со второго этажа теоротдела еще раздавались громкие голоса, да и просто крик, которые посторонний мог бы принять за выяснение отношений.
А там всего лишь Аркадий и Миша вместе с соавторами выясняли свои отношения с природой. За 40 лет ничего, кроме цвета волос, не изменилось. И сейчас всё то же самое происходит в Институте теоретической физики в Миннеаполисе. Их увлеченности наукой могут позавидовать первокурсники. Эти же слова относятся и к Натану Зайбергу.
Нельзя не упомянуть о той исключительной роли, которую играл, да и продолжает играть Аркадий в «воспитании» более молодых теоретиков. У него мало формальных учеников, но очень многие, включая автора этих строк, прекрасно понимают, как много он им дал. «Радиус Вайнштейна», величина, известная в теории гравитации, прямо скажем, довольно велика.
Как сказал один коллега, конференции делятся на скучноватые, на проходящие довольно живо и на те, в которых принимает участие Вайнштейн. А Миша Шифман в последние годы передает свою увлеченность наукой в книгах и очерках, где истории ученых и научных идей читаются как захватывающие детективы. Их роль в передаче «факела научных знаний» велика, и отчасти из-за отъезда таких людей проблема с институтами научной репутации и экспертизы в России столь серьезна.
На этом мы закончим короткую прогулку по флуктуирующему вакууму. Как уже было сказано, проблема конфайнмента в КХД пока устояла и ждет своего решения. Более того, оказалось, что она тесно связана с проблемой построения квантовой гравитации, но это уже другая история.

Результаты лауреатов чрезвычайно важны и, несомненно, будут одними из ключевых элементов при нахождении ответа. Лауреатов у премии Дирака может быть всего трое, это ограничение при присуждении премии, поэтому я не сомневаюсь, у комитета были трудности с выбором из несколько более широкого списка. Совершенно необходимо отметить и научный вклад Валентина Захарова, Никиты Некрасова и Виктора Новикова. Еще раз поздравляю трех лауреатов с этой заслуженной наградой.

С точки зрения обычного читателя, в целом, понятно о чем речь, но сложно, не хватает базовых знаний, что бы это действительно понимать.
«Четырехмерный мир», лучше в кавычки, время, все же не измерение, как бы ни красиво это звучало.
Сложными вопросами задавались ребята, хорошо что хоть где-то за это платят и наука движется вперед, пусть даже, применение этому найдут только через 100 или 1000 лет.
Далее, на правах дилетанта.
Если Вы в этой теме, предлагаю оценить вероятность изменения мерности при условии постоянного расширения. То есть, если вселенная расширяется, при неизвестной плотности базовой среды (на самом нижнем уровне) вовне от места последствия предполагаемого большого взрыва, предполагая что расширение будет продолжаться, а плотность снизится например еще в 20 раз, то изменится ли мерность пространства?. Предполагаю, что ранее, при большей плотности, мерность была значительно выше, в зависимости от возможного предела взаимодействий минимальных универсальных частиц, при числе взаимодействующих частиц X, мерность = X-1. И если это так, то в случае продолжения изменения плотности, «мерность» будет снижаться. Соответственно, если вселенная неоднородна, то в местах большей плотности, могут существовать более многомерные пространства, а меньшей — менее многомерные.
Теоретические расчеты касаемые числа измерений более 3-х, во многом касаются сегодняшнего предела. Проверить, действительно ли мы существуем в 6 или 11-мерном пространстве, можно только измеряя скорость и положение при перемещении в наших трех измерениях более многомерной частицы (кластера из частиц), ее флуктуацииями в зависимости от происходящих воздействиях, но это еще сложнее чем поймать гравитационную волну, хотя, не исключено, что именно таким образом, засекая не только волну но и ее «отражения», сможем «увидеть», сколько же измерений у нашего пространства, а так же, возможно, на каких же «гранях» мы существуем.
Статья ,написанная в стиле научно-популярного жанра,отражает современный подход к пограничным областям теории гравитации и полезна как специалистам,так и обывателю интересующемуся развитием науки.
В древности мыслителей не смущало, что мир является конечным и бесконечным одновременно. Не исключено, что мир является бесконечномерным многообразием.
Мне пришлось столкнуться с темой обнаружения суперсимметрии в результате раскрытия механизма получения катализатора для холодной трансмутации ядер. Без сомнения верно, что процесс вызывается проиходящими флуктуациями физического вакуума в результате чего происходит рождение атомного коллапсара-монополиума, являющегося квантом тёмной материи и катализирующего реакции холодной трансмутации ядер за счёт магнитно-монопольного эффекта. Коллапсар имеет состав:кольцевая сингулярность из двух гравитинных струн с мнимой массой, заключённых во внутренний сферический и горизонт, состощих из пары колец массивных гравитонов, который, в свою очередь, находится внутри внешнего горизонта, образуемого парой флаксонов (бион). Дуальность Зайберга имеет место и в моей гипотетико- дедуктивной модели квантовой гравитации. В частности, для образования двух гравитонов используется два синглетных майорона(аксион) и один бозон Хиггса с положительной массой. Для получения двух гравитино берутся два снейтрино (дублетный майорон, годстино…) и один вновь синтезированный тахионный бозон Хиггса. В модели обычный бозон Хиггса компенсирует тахионный бозон Хиггса, что приводит а безмассовому состоянию тёмной материи. Наличие темной материи в виде магнитного поля планеты доказывает её присутствие.