(Сахаров и космология)

В предыдущей статье, посвященной вкладу Андрея Дмитриевича Сахарова в космологию, (ТрВ № 79), речь шла о барионной асимметрии Вселенной и его пионерской работе на эту тему. Сейчас мы рассказываем о более ранней, тоже пионерской работе, в которой был теоретически предсказан эффект, получивший впоследствии название «Сахаровские осцилляции». Обе работы в какой-то степени опередили время, обе были частично основаны на неправильных предположениях, но тем не менее верны в принципе, обе имели далеко идущее развитие в последующие десятилетия.
Распределение материи в современной Вселенной неоднородно на масштабах до примерно 100 мегапарсек (300 миллионов световых лет). Она выглядит как гигантская застывшая пена типа монтажной, используемой для установки окон: почти пустые пузыри (так называемые войды) и стенки. Откуда взялась эта структура? Ясно, что она — результат гравитационной неустойчивости — той же самой, что заставляет облака космического газа и пыли сгущаться в звезды. Задолго до открытия этой структуры Я.Б. Зельдович теоретически показал, что гравитационная неустойчивость в ранней Вселенной должна дать именно такую пену (пересекающиеся «блины» в терминологии Зельдовича с коллегами) в результате роста первоначальных возмущений плотности, неясен был только ее масштаб. Реальная картина прорисовалась только к концу 80-х, когда «пена» прорисовалась на трехмерных картах скоплений галактик по данным обзоров. Но главный вопрос оставался: из каких начальных возмущений сконденсировалась «пена» крупномасштабной структуры Вселенной?

Работа А.Д. Сахарова, о которой идет речь, делалась в первой половине 60-х годов и была опубликована в 1965 г. Тогда про крупномасштабную структуру ничего не знали. Но все равно стоял вопрос: как возникли скопления галактик и сами галактики, откуда взялись начальные возмущения, из которых они сгустились?
В то время не знали многих других вещей: еще не была сформирована концепция раздувающейся Вселенной, еще не было открыто реликтовое излучение. Последнее обстоятельство делало теорию горячей Вселенной недоказанной гипотезой, что позволяло предполагать, что Вселенная родилась плотной, но холодной. Модель горячей Вселенной была популярной, но Я.Б. Зельдович, чей авторитет в космологии был бесспорен, в то время пропагандировал модель холодной Вселенной.
Исходные предположения А.Д. в данной работе таковы:
1. Первоначальные возмущения плотности в ранней Вселенной имеют природу квантовых флуктуаций. Это предположение и поныне лежит в фундаменте космологии.
2. Возмущения возникли в самом начале Большого взрыва, при планковской плотности, когда сильны эффекты квантовой гравитации, и дальше эволюционировали в соответствии с расширением Вселенной. По наиболее популярным современным представлениям, это не так: возмущения, определившие «лицо» Вселенной, возникли позже — на стадии экспоненциального раздувания (инфляции) Вселенной. Принципиальной разницы здесь нет, однако раздувающаяся Вселенная позволяет решить еще другие проблемы космологии, которые А.Д. в своей статье не рассматривал.
3. Изначально температура Вселенной равна нулю. Это ошибочное предположение, которое, по признанию самого А.Д., сильно снизило ценность работы. Оно сделано под влиянием Я.Б. Зельдовича, на которого А.Д. ссылается в своей статье по этому поводу. Однако эта ошибка не стала фатальной, поскольку уравнения состояния (связь между плотностью энергии и давлением) в горячей и холодной моделях совпадают до некоторого момента.
Из физики первых мгновений
Что происходит с первичными возмущениями при расширении Вселенной? Они становятся акустическими волнами, двигающимися со скоростью звука, участвуя в общем расширении. Хорошо известно, чему равна скорость звука в самой ранней Вселенной: с/7(3), где с — скорость света. Это результат так называемого ультрарелятивистского уравнения состояния, когда давление в среде равно одной трети плотности энергии, p = e/3. Последняя включает энергию покоя частиц, поэтому в разреженном газе из холодных, а значит медленных, частиц давление много меньше плотности энергии, а скорость звука много меньше скорости света. Наоборот, ультрарелятивистское уравнение состояния возникает, когда в среде частицы двигаются со скоростью, близкой к скорости света.
В горячей Вселенной ультрарелятивистское уравнение состояния держится довольно долго — около 300 тыс. лет. Первые доли секунды оно поддерживается за счет того, что все частицы двигаются почти со скоростью света из-за высокой температуры. Потом температура падает настолько, что протоны становятся нерелятивистскими (движущимися существенно медленней скорости света). Однако они выгорают, проаннигилировав с антипротонами, их число уменьшается на девять порядков величины (см. предыдущую статью в ТрВ-Н № 79, http://trv-science.ru/2011/05/24/). Дальше в течение секунд во Вселенной доминируют безмассовые фотоны и легкие электроны с позитронами. Последние тоже аннигилируют друг с другом, когда становятся нерелятивистскими, при этом электронов тоже остается одна миллиардная от их прежнего числа. Далее в плотности энергии Вселенной доминируют фотоны. Протоны хоть и тяжелые, но их в миллиард раз меньше — многочисленные фотоны поддерживают ультрарелятивистское состояние еще около 300 тыс. лет. Тогда же, через 370 тыс. лет после Большого взрыва, происходит еще одно важное событие, но об этом — ниже.
В холодной Вселенной работает совсем другая физика, которая тоже обеспечивает ультрарелятивистское уравнение состояния, но только первые доли секунды. Это чисто квантомеханический эффект, в его основе лежит принцип Паули, запрещающий двум протонам или двум электронам находиться в одном квантомеханическом состоянии.
Тот же самый принцип не дает всем электронам в атоме сесть на низший энергетический уровень. В плотном газе принцип Паули тоже заставляет электроны распределяться по разным энергиям (точнее, по импульсам, где направление тоже имеет значение).
Если температура равна нулю, частицы равномерно заполняют объем сферы в пространстве импульсов. Такой газ частиц называют вырожденным Ферми-газом, а максимальную энергию частиц, ниже которой весь фазовый объем заполнен,— энергией Ферми. Чем больше плотность, тем выше энергия Ферми. Если энергия Ферми много больше энергии покоя частицы, имеем p = e/3 даже при нулевой температуре.
Через доли секунды после начала расширения холодной Вселенной энергия Ферми становится меньше массы протона, и скорость звука падает практически до нуля.
В общем, с точки зрения акустики, начальные этапы расширения в холодной и горячей Вселенной качественно похожи: уравнение состояния то же самое, скорость звука та же самая, и там и там происходит переход к нерелятивистскому уравнению состояния, только в очень разное время.
Стоячие волны
Итак, вначале были квантовые первичные возмущения плотности. Они стали распространяться по Вселенной, как звуковые волны, со скоростью, сравнимой со скоростью света.
Любые колебания, подчиняющиеся линейным дифференциальным уравнениям, будь то звук или свет, можно смело раскладывать на волны разных длин и смотреть по отдельности, что происходит с каждой из них.
Для начала допустим,что некая вселенная внезапно возникла, будучи в целом однородной, но с локальными возмущениями плотности? и не расширяется (это внутренне противоречивая картина, но мы ее используем лишь для иллюстрации). Начальные неоднородности, если они были хаотическими (случайными), превратятся в волны, разных длин складывающиеся в хаотическую картину. Спектр этих волн в произвольный момент времени примерно повторяет спектр начальных возмущений, хаос остается хаосом. Но может быть более интересная ситуация: волны могут оказаться стоячими.
Пример стоячей волны — колебания струны на гитаре. Вся струна в один момент выпрямляется, через четверть периода максимально изгибается, потом снова целиком выпрямляется и т.п. В случае со струной «стоячесть» колебаний обеспечивается закрепленными концами. Другой пример: стоячие волны около бетонной стены причала в порту. Точно так же на одном и том же месте то возникают высокие волны, то поверхность воды разглаживается. Там нет закрепленных концов, но есть отраженная волна, которая, суммируясь с набегающей, дает стоячие волны.
Любую карту начальных возмущений можно разложить в ряд Фурье, члены которого будут иметь вид плоских волн: Ck cos(xk + фк), где x — координата, k — волновой вектор фк — фаза. Решение волнового уравнения для звуковых колебаний хорошо известно: каждому члену разложения будут соответствовать плоские волны: С cos(xk — t+ф.). Здесь v — частота колебаний волны, которая связана с волновым вектором через скорость звука v: v = k v.
Если скорость вещества вначале равна нулю, то начальные возмущения статичны, т.е. они не зависят от времени. В этом случае волны можно сгруппировать по симметричным парам с противоположно направленными волновыми векторами: 0.5 Ck cos(xk — tv+ φk) + 0.5 Ck cos(–xk — tv-φk) (т.е. Ck = С-k, φk = –φk).
Действительно, положив t = 0, получаем исходное разложение, а продифференцировав по времени, получаем нуль при t = 0. Наконец, разложив косинус суммы двух углов, получаем стоячие волны вида Ck cos(xk + фк)cos(tv), т.е. амплитуда волн с данной частотой будет синхронно и периодически меняться во всем пространстве.

Оказывается, и в целой вселенной можно получить стоячие звуковые волны. Самая простая возможность (хотя и не единственная) — потребовать, чтобы все начальные возмущения во вселенной были статичными, т.е. начальные скорости вещества в них были равны нулю. Тогда все возникшие волны можно будет разбить на противоположно направленные симметричные пары плоских волн — как волны у стены причала, и их сумма даст именно стоячие волны,синхронно исчезающие и вырастающие во всем пространстве. Чтобы проверить это самому, достаточно знаний курса общей физики и умения разлагать косинус суммы двух углов (см. врезку).
Какой будет картина звуковых колебаний плотности во вселенной в случае стоячих волн? На глаз она по-прежнему будет казаться хаотичной, но если построить спектр флуктуаций плотности в пространстве (для этого надо карту плотности среды во вселенной подвергнуть преобразованию Фурье), то выявится удивительная вещь: он периодичен!
Спектр неоднородностей в зависимости от их размера L будет пропорционален cos(p T v/L), где Т — возраст вселенной (считаем, что скорость звука v не зависит от времени). Из этой зависимости можно оценить возраст своей вселенной! Однако наше требование о том, чтобы все начальные возмущения плотности были статичными в придуманной нами статичной вселенной, ниоткуда не следует.
Как обстоит дело в расширяющейся вселенной? Основные отличия таковы:
1. Каждая волна будет участвовать в расширении, и ее длина и частота будут меняться.
2. Условие статичности начальных возмущений выполнится автоматически! Дело в том, что вначале вселенная расширяется столь быстро, что начальные скорости вещества быстро забываются, тогда как амплитуды волн остаются прежними. Это значит, что все звуковые колебания плотности в ранней вселенной будут иметь вид стоячих волн — при одинаковой частоте синхронно во всем пространстве достигать максимума и обращаться в ноль. Это утверждение прямо следует из работы А.Д. Сахарова. Зависимость амплитуды волн от времени получается несколько более сложной, чем косинус, — она выражается через функции Бесселя, которые тоже осциллируют в зависимости от длин волны.
Волны застывают
Давление среды во Вселенной рано или поздно в некое время T становится много меньше плотности энергии, и скорость звука сравнительно быстро падает на порядки. Акустические волны становятся застывшими неоднородностями плотности, причем они застывают практически одновременно — независимо от длины волны. И эту картину застывших волн можно попытаться увидеть, если как-то суметь снять карту неоднородностей и разложить ее в ряд Фурье.
Что мы должны увидеть? «Застывание» всё-таки происходит не мгновенно, поэтому короткие волны успевают усредниться, пока скорость звука падает. Значит, коротковолновая часть спектра будет невыразительной, лишенной каких-то особенностей. А более длинные волны, которые успели совершить ровно одно-два-три-четыре колебания с рождения Вселенной, проявятся в спектре в виде четких максимумов, разделенных провалами. Еще более длинные волны, которые не успели совершить ни одного колебания, опять дадут плавную часть спектра, лишенную особенностей. Именно такая картина получила название «Сахаровские осцилляции». Правда, именной термин используется далеко не всеми, в настоящее время чаще используется его синоним «акустические осцилляции».
Когда происходит застывание, и на каких масштабах оно должно проявиться? В варианте холодной Вселенной, как уже было сказано, скорость звука падает через доли секунды. При этом самый длинноволновый максимум в спектре неоднородностей охватывает массу вещества порядка массы небольших звезд.
В том же 1965 году, когда была опубликована данная работа А.Д. Сахарова, было открыто реликтовое излучение, однозначно свидетельствующее о том, что Вселенная родилась горячей. В связи с этим потребовался новый анализ акустических осцилляций. Это сделали независимо Я.Б.Зельдович с Р.А.Сюняевым (R. Sunyaev, Ya. Zeldovich. Astrophysics and Space Science vol. 7 (1970), p.3) и Peebles с J.T.Yu (PJ.E. Peebles, J.T. Yu. Astrophysical Journal vol. 7 (1970), p.815). Как уже сказано выше, в горячей Вселенной скорость звука падает примерно через 300 тыс. лет. При этом в самый длинноволновый пик, соответствующий одному колебанию, оказываются вовлечены массы порядка 1018 масс Солнца: десятки миллионов галактик.
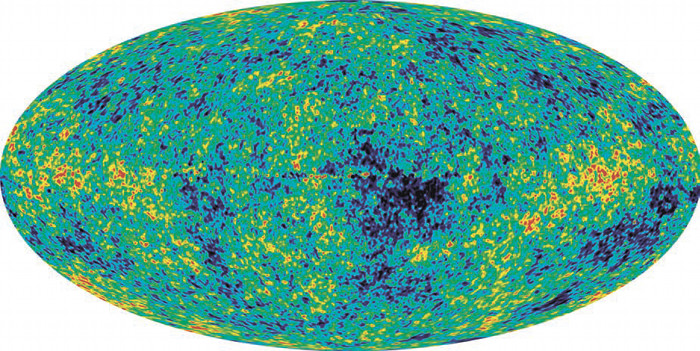
Горячая модель дает еще один сюрприз — фотографию Вселенной возраста 370 тыс. лет — как раз той эпохи, когда уравнение состояния Вселенной менялось и скорость звука падала. Дело в том, что в это время температура Вселенной упала настолько, что электроны с протонами рекомбинировали в атомы водорода и Вселенная стала прозрачна для света. Этот свет из-за расширения Вселенной превратился в радиоволны — знаменитое реликтовое микроволновое излучение.
Улыбка Мироздания
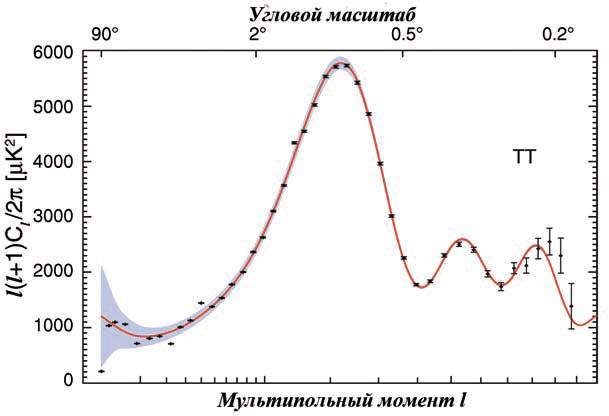
Если бы А.Д. Сахаров увидел спектр мощности угловых гармоник реликтового излучения! (Он изображен на рис. 2.) Я. Б. Зельдовичу тоже не довелось его увидеть, зато многие, принимавшие непосредственное участие в развитии теории, дожили.
Мощь науки ярче всего проявляется не тогда, когда удается объяснить ранее непонятный эффект, а когда кто-то предсказывает нечто неординарное и потом это находят воочию. Крупных примеров подобного рода в истории не так уж много. Хрестоматийный пример — открытие Нептуна «на кончике пера».
Сахаровские осцилляции в некотором плане куда «круче», прежде всего своей запредельностью — непредставимостью масштабов, как непредставимо маленьких, так и непредставимо больших. Сидит человек и пишет формулы с невероятными цифрами: возраст Вселенной — 10-43 секунды, плотность —1098 грамм на см3, что-то из них пытается вывести. Откуда убеждение, что на таких масштабах вообще работает наша логика, что к ним применимы законы, выведенные человеком? С точки зрения постороннего, ученый в данном случае занимается полными абстракциями, фантазиями на деньги налогоплательщиков. В результате значительных усилий человек выводит на бумаге, что распределение неких флуктуаций плотности во Вселенной должно описываться некой осциллирующей функцией Бесселя.
Через десятилетия люди запускают космический аппарат с прецизионным приемником микроволнового радиоизлучения, испущенного миллиарды лет назад. И видят из карты этого излучения ту самую осциллирующую функцию Бесселя!
Наблюдение самого факта акустических осцилляций — только начало. Оказывается, они лучше, чем что-нибудь другое, помогают измерить целый ряд параметров нашей Вселенной, включая ее возраст и геометрию. Это примерно то же самое, как если бы на карте ранней Вселенной увидели бы масштабную линейку с делениями в мегапарсеках, да и не только линейку — часы и целую «метеостанцию» с различимыми показаниями на циферблатах.
Например, высота главного пика над подложкой дает оценку плотности вещества во Вселенной, а положения пиков «чувствуют» геометрию пространства. Последнее свойство нетрудно понять: длина акустической волны, попавшей в максимум через 370 тыс. лет после Большого взрыва, фиксирована, а угол, под которым она сегодня видна, зависит от того, евклидово наше трехмерное пространство или нет. Именно из измерений положений пиков следует, что пространство на самом деле евклидово: сумма углов треугольника составляет в нем 180°, даже если речь идет о треугольниках со сторонами в десятки миллиардов световых лет.
Сахаровские осцилляции — не единственная зацепка для космологов — есть еще далекие сверхновые, скопления галактик, гравитационное линзирование. Но это, безусловно, самая надежная опора.
Мы рассказали всего о двух научных работах Андрея Дмитриевича Сахарова. Это лишь небольшая часть из того, что он сделал за свою жизнь. Однако даже по двум работам можно судить о мощи этого человека: в них не просто решены какие-то проблемы. В этих работах поставлены и решены проблемы, которые еще никто не видел в то время.
Валерий Рубаков,
Борис Штерн