Доклад на конференции в рамках «Дней науки»
(организатор — Фонд «Династия», СПб, 21-23 мая 2009 г.)
Вообразите Париж 20-х годов — столицу модернизма и мировой моды. Коко Шанель, вспоминая это время, рассказывает Полю Морану о Пикассо: «Я восхищалась его живописью, хотя не понимала ее. Но я находила ее убедительной, а это то, что я люблю. Для меня это как таблица логарифмов».
Вдумайтесь в эту удивительную параллель. Математика абстрактна, живопись Пикассо абстрактна; казалось бы, вот самое очевидное сходство между двумя непонятностями: «Девушка с обручем» (1919) и «Таблица логарифмов». Но Шанель выбирает другое слово: обе «убедительны», а убедительность — это то, что ее привлекает.
* * *
В рамках этого доклада, посвященного разным языковым аспектам содержания и формы математической деятельности, я постараюсь уделить специальное внимание этому качеству — «убедительности».
На личностном уровне убедительность доказательства, идеи, компьютерной симуляции зависит от предрасположенности математика к геометрическому или логическому мышлению, философских склонностей (возможно, неосознаваемых), наконец, ценностной установки.
В социальном плане в игру вступают крупномасштабные исторические обстоятельства, которые могут способствовать как поразительному расцвету математики, так и ее практическому исчезновению.
По понятным причинам историки математики обращаются к тем местам и временам, где математика создавалась или хотя бы принималась по наследству. Но очень интересно было бы пристально вглядеться в исторические обстоятельства ее неприятия, вплоть до (временного) ухода со сцены.
Развитие античной, главным образом греческой, математики в Европе прервалось по крайней мере на первую тысячу лет христианства. Ho еще до христианства практичные и воинственные римляне, создав высокую цивилизацию, интегрировали в нее греческую гуманитарную культуру, но не греческую науку. Даже очевидные военные приложения не смогли соблазнить их. Согласно Плутарху, при осаде Сиракуз римский генерал Марцелл тщетно призывал своих солдат не отступать перед «этим геометрическим Бриареем» (Архимедом), который со своими военными игрушками «превосходит сторуких гигантов мифологии!»
Впрочем, сам Архимед не считал свои инженерные свершения «приложением» своей математики: для его могучего ума они были отвлечением от математики, которого он предпочел бы избежать.
* * *
Скудное математическое наследие античного Рима включает дошедшую до наших дней систему обозначения целых чисел:
I, II, III, IV, V, VI, VII, VIII, IX, X, XI,…, L,…, C,…, D,…, M.
Поучительнее всего рассматривать ее как уникальную археологическую коллекцию следов архаического состояния математической мысли.
Единица I символизирует зарубку на посохе (не латинскую букву I — это позднее переосмысление). Усилие, уходящее на каждую зарубку, и занимаемое ею место на, скажем, пастушеской палке, заставляет переходить от тупой, но предельно систематической и потенциально бесконечно продолжимой системы обозначения чисел
I, II, III, IIII, IIIII, IIIIII, . . .
к гораздо более непоследовательной (и не позволяющей уйти в бесконечность), но поначалу экономной и уютной системе скорее «имен», чем символов (так же в начальном отрезке прослеживаемой до зарубок):
I = 1, V = 5, X = 10, L = 50, C = 100, D = 500, M = 1000.
Короткие последовательности этих примарных символов интерпретируются с помощью сложения, иногда вычитания: 2009 = MMIX = M + M — I + X. Конечно, нуль не имеет имени. Ужас перед «отсутствием», «пустотой», глубоко укоренен в человеческой психологии. Еще Экклезиаст сказал: «Чего нет, того нельзя считать».
Невозможность обозначить нуль критически мешает развитию системы и превращению ее в позиционную.
* * *
Распространение позиционной системы записи чисел в Европе после выхода книги Леонардо Фибоначчи Liber Abaci (1202) было в сущности началом экспансии единственного действительно глобального мирового языка. Семантикой этого языка был счет чего угодно: зарубок, скота, кораблей, флоринов… Его ядерный синтаксис определялся универсальным правилом перевода абстрактного количества в позиционную (десятичную) запись и обратно. Наконец, его прагматика имела две стороны. Когда референтом текста, состоящего из чисел, был фрагмент внешнего мира, скажем торговля, важным связующим звеном между текстом и внешним миром становились синтаксические правила более высокого уровня. Знаменитый пример таких правил — система двойной бухгалтерии, кодифицированная Лукой Пачиоли в 1494 г.
Когда референтом числового текста служили данные научных, например астрономических, наблюдений, его прагматика могла быть связана с предсказанием, скажем, затмения или построением количественной модели Солнечной системы. В этом случае текст должен был подвергнуться алгоритмической переработке. Иными словами, он служит входом для некоторой программы, тогда как ее выходом становится новый числовой текст, опять имеющий референтом наблюдаемый мир.
Неоценимым достоинством позиционной системы была ее идеальная приспособленность к такой алгоритмической переработке, в частности простые и универсальные правила сложения и умножения, которым можно было научить школьников и клерков. Более сложные программы — инструкции клеркам — описывались на естественном языке как итерация элементарных алгоритмов с добавлением условных переходов («если дебит клиента NN превзойдет его кредит на ZZ флоринов, прекратить поставки»).

Язык программ очень долго существовал лишь как неформализованный поддиалект естественного языка с очень ограниченной (хотя критически важной) сферой применимости. Еще Алан Тьюринг, уже в XX в., мотивируя свою универсальную формализацию вычислимости, когда говорил «компьютер», подразумевал человека, механически следующего конечному списку лежащих перед ним инструкций.
Парадоксальный пример такой деятельности, ставший культурно-историческим памятником общецивилизационного масштаба, — 90 страниц таблиц натуральных логарифмов Джона Непера, опубликованные в его работе Mirifici Logarithmorum Canonis Descriptio,1614 (интуиция Коко Шанель и здесь не обманула ее). Логарифмы были вычислены знак за знаком, вручную. Конечно, Непер соединял в одном лице роль творца новой математики и клерка-компьютера, следующего собственным инструкциям.
Тем поразительнее философское прозрение Лейбница, его знаменитое Calculemus!, постулирующее, что не только манипуляции с числами, но любое строгое и логически последовательное рассуждение, выводящее умозаключение из принятых посылок, должно быть сводимо к вычислению.
Нанесение на карту точных границ лейбницевского идеального мира, в котором рассуждение эквивалентно вычислению, истинность может быть формализована, но не всегда может быть формально удостоверена, где с предельной ясностью можно увидеть, как даже самая малая канторовская бесконечность (натуральных чисел) ускользает из объятий конечно порожденного языка, и было высшим достижением великих логиков ХХ в. (Гильберт, Черч, Гедель, Тар-ский, Тьюринг, Марков, Колмогоров…).
Центральное понятие этой программы, формальный язык, унаследовало основные черты как естественных языков (фиксируемых посредством алфавитной письменности), так и позиционной системы записи чисел и арифметики. В частности, любой классический формальный язык одномерен/линеен, состоит из дискретных символов, эксплицитно выражает базисные логические средства.
Любой реальный математический текст состоит из слов с вкраплениями формул. Формулы можно считать выражениями формального языка (он может меняться от статьи к статье, но часто представляет собой просто версию языка теории множеств).
Вопрос о том, как слова и символы делят между собой функцию передачи содержания, заслуживает отдельного обсуждения. Важнее всего, что слова адресуют работу людям, а не читающим автоматам; они же занимаются такими тонкостями, как выражение системы ценностей автора.
Формулы не всегда и не везде являются носителем смысла в ядерных фрагментах математического текста. По крайней мере со времени Евклида и до наших дней в школьных учебниках геометрии роль формул играют чертежи. Многие помнят рисунок квадрата, разделенного двумя линиями на два меньших квадрата и два прямоугольника. Этот чертеж иллюстрирует/заменяет/доказывает формулу (а + b)2 = а2 + 2ab + b2.
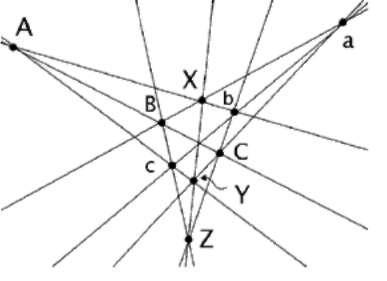
Гораздо интереснее — и гораздо менее известен — чертеж, иллюстрирующий античную теорему Паппа Александрийского (около 300 г. н. э.).
Пользуясь им, удобно проиллюстрировать, как геометрическое мышление математиков взаимодействует с формульным и формальным, причем на протяжении многих поколений.
Прежде всего — о содержании теоремы.
Начнем с плоского шестиугольника, на чертеже его вершины BXbCYc. (Он не обязан быть выпуклым, как на картинке! Вот первая ловушка чертежей — они часто заставляют принимать неосознанные ограничения.)
Любая пара противоположных сторон шестиугольника, скажем Bc и bC, определяет также промежуточную между ними диагональ XY. Продолжим эти две стороны и диагональ; может оказаться, что три прямые пересекутся в одной точке.
ТЕОРЕМА ПАППА. Если это свойство выполняется для двух пар противоположных сторон шестиугольника, то оно выполняется и для третьей пары.
Это удивительный результат. Прежде всего, трудно вообразить себе, как к нему можно было прийти. Он не принадлежит евклидовой геометрии: расстояния, длины и углы не играют в его формулировке и доказательстве никакой роли; не играет роли также группа эвклидовых движений плоскости. Единственные структурные отношения примитивны: плоскость состоит из точек; прямые — это некоторые подмножества точек; две прямые пересекаются ровно в одной точке; через две точки проходит одна прямая.
Только в XIX в. было понято, что теорема Паппа — центральный результат плоской проективной геометрии. Сначала это была геометрия обычной плоскости над вещественными числами. Потом открылось, что то же верно для проективной плоскости над любым абстрактным полем; это поле, его законы композиции и аксиомы — всё восстанавливается по конфигурациям Паппа.
Наконец, ближе к концу XX в. оказалось, что эквивалентность теоремы Паппа с теорией коммутативных полей объясняется и обобщается в широком контексте теории моделей. Модель формального языка есть, попросту говоря, отображение этого языка в язык теории множеств вместе со стандартной интерпретацией последнего. Так смысл изысканного чертежа проявляется в сложной метаязыковой конструкции.
Чертежи не поддаются объединению в язык по многим причинам. Синтаксис чертежей прихотлив и не систематичен, синтаксические связи между ними сопротивляются формализации, чертежи обладают целостностью, которая утрачивается при анализе. Их функция в разных процессах передачи и хранения информации отличается от функции даже «синонимичных» языковых конструкций, они взывают к другому типу воображения, к право-полушарной интуиции.
Когда с развитием гомологической алгебры и теории категории во второй половине ХХ в. в математику стали внедряться «чертежеподобные» языковые конструкции, коммутативные диаграммы, должен был пройти некоторый период привыкания к ним.
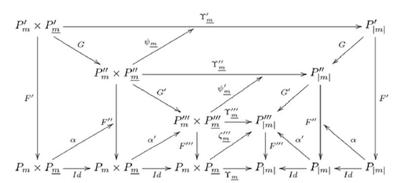
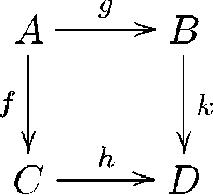
На рис. 2 изображена такая диаграмма (вполне реалистическая: из работы Д.Борисова и автора, 2007 г.). Элементарной составляющей диаграммы является коммутативный квадрат. До эры категорий линейная языковая запись утверждения, выражаемого этим квадратом, почти исчерпывалась бы равенством h ◦ f = k ◦ g. Но это верно лишь с существенной оговоркой: f, g,h,k здесь — морфизмы в категории, и необходимо знать, из какого объекта в какой каждый морфизм «бьет».
Более того, в большой диаграмме на рис. 2 можно увидеть косые стрелки, вроде а. Такая стрелка изображает морфизм не в исходной категории, скажем C, где живут объекты, имена которых отмечают начала и концы стрелок. Она изображает морфизмы в категории морфизмов Mor C:
а : Id ◦ F’- F» ◦ G.
Точное содержание диаграммы можно передать лишь подробно откомментировав ее обычным линейным текстом, перемежающим слова и формулы. Но делает ли такой текст излишней самое диаграмму? Нет! (Я переписывался с коллегой по электронной почте, обсуждая вполне конкретный математический сюжет. В тексте e-mail, конечно, приходится обходиться словесными экивоками. Вдруг я получаю от своего корреспондента вопль души: «Диаграмму! Полцарства за диаграмму!»)
Ниже я намерен аргументировать точку зрения, согласно которой, развитие теории категорий, и в особенности гомотопической топологии, в течение последних десятилетий не только было существенным прогрессом конкретной области математики, но также способствовало осознанию и вербализации происходящего на наших глазах эпистемологического сдвига в том, что принято было называть «основаниями» математики.
Я должен оговориться: для меня «основания» лишены прескриптивной или нормативной функции. Я понимаю под «основаниями» плод работы математиков, которые склонны вглядываться в практику выбора задач, оформления доказательств и экспериментов, в ценностные ориентации живущих и ушедших поколении математиков.
Важнейшая социальная функция исследований, посвященных основаниям, состоит в поддержании диалога между «двумя культурами» (Ч.П.Сноу). Диалог этот начинается потому, что математика постоянно вызывает естественное философское беспокойство. Если не принимать буквально существование объективного, независимого от нас платоновского мира идей (а философы иногда готовы не принимать даже существования мира вещей и явлений), то придется признать, что математика есть просто плод высокотренированного воображения нескольких тысяч человек в каждом поколении.
Тогда, даже оставив на время заботу о критериях «истинности» математических утверждений, нельзя не поразиться упрямой устойчивости математического знания, его межпоколенческой и межцивили-зационной воспроизводимости.
Больше того, это знание не просто воспроизводится, как воспроизводятся тексты «Одиссеи», «Гильгамеша» или Евангелия. Оно развивается и обогащается, в последние 200 лет — с неслыханной прежде скоростью.
* * *
Возвращаясь к проблеме математического содержания «оснований математики» и его исторической эволюции за последние полторы сотни лет, я представлю ее следующим образом.
Исходным ментальным образом, общим для огромного большинства работающих математиков после, скажем, Второй мировой войны, является образ множества с дополнительной структурой: топологического пространства, группы, кольца, пространства с мерой…
На первых ступеньках это множество является чисто канторовской абстракцией: природа его элементов не важна, важно лишь, что они попарно различимы и мыслятся как объединенные в единое целое. На следующих этапах элементы нового множества могут быть открытыми подмножествами предыдущего, локальными функциями на нем и т.п.
Сам Кантор в минималистком вдохновении задал самые базисные вопросы о таких множествах, продемонстрировал бесконечную шкалу бесконечностей и оставил нескольким поколениям логиков задачу разбираться с онтологией и гносеологией этой шкалы.
Более прагматичное поколение, пережившее первую войну, построило на этом потенциально метафизическом фундаменте архитектурно современное и функционально эффективное здание работающей математики из индустриально производимых элементов под названием «структуры» в смысле Бурбаки.
Вопросы о шкале бесконечностей ушли для работающих математиков на задний план, но дискретные множества как основной строительный материал остались. Непрерывное стало надстройкой над дискретным.
Между тем, еще до Кантора некоторые проблемы со строительством из множеств даже элементарной арифметики были совершенно ясны. Если натуральные числа именуют количества палочек или любых конечных дискретных множеств,
I, II, III, . . .
то уже нуль как мощность пустого множества создает психологические проблемы, а отрицательные числа требуют или искусственной алгебры, или интерпретации в совершенно другом универсуме, скажем экономических отношений («долг»).
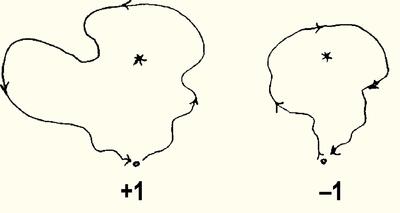
Вместе с тем, если исходным элементом интуиции считать непрерывное, а дискретное вводить как производную структуру, то целые числа получают удивительно естественное воплощение. Вообразите точку, движущуюся по плоскости. Пусть она выходит из какой-то начальной позиции, блуждает некоторое время, а потом возвращается назад, ни на момент не попадая, скажем, в начало координат. Вопрос: сколько раз она обойдет вокруг начала? Нетрудно дать точное определение этому целому числу: оно может быть нулем, положительным или отрицательным (обходы бывают по часовой стрелке, а бывают — против).
Более того, нетрудно понять, как обходы сначала в одну сторону, а потом в другую сокращаются (1 — 1 = 0): путь, состоящий из двух таких обходов, можно стянуть в точку, не задевая начала координат.
Так что же было вначале, дискретное или непрерывное? Конечно, это архетипический вопрос философии: ijoyoq, вероятно, символизирует дискретное, а хао? — непрерывное.

Пользуясь метафорой из смежной профессии, этнографии, я сравнил бы эту ситуацию с теорией мифа по Леви-Строссу. Не без влияния Бурбаки Леви-Стросс сконструировал интерпретацию мифа как медиации оппозиции. Обдумывая его концепцию четверть века назад, я предположил эволюцию в обратном направлении: согласно этому взгляду, миф отмечает эпоху, когда осознание оппозиции («дискретного») рождалось из ментального хаоса. Так музыкальная нотация рождалась из самой музыки.
* * *
Способ вводить целые числа, который я набросал выше — считать количество обходов с учетом ориентации, которые делает замкнутый путь на плоскости вокруг начала координат, — начал свое существование как одна из самых ранних теорем гомотопической топологии.
Геометр, занимающийся гомотопической топологией, видит умственным взором бесконечномерные пространства, которые могут деформироваться и должны деформироваться вплоть до стягивания в одну точку. В конечном счете дискретность, которую тополог вычисляет и передает дискретным языком, сводится к «связным компонентам» этих пространств и производных от них пространств отображений.
В популярных изложениях математики, а теперь и в видеофильмах «узлы» в R3, или «выворачивание сферы наизнанку», используются, чтобы экстериоризировать такие приватные ментальные образы. Возможности этой экстериоризации как учебного средства ограничены, так же как ограничена возможность вообразить себя Святославом Рихтером, исполняющим Шуберта, посмотрев его интервью с Бруно Монсенжоном.
Поэтому я смогу лишь вкратце изложить свои впечатления об эпистемологическом сдвиге, динамику которого я различаю в основаниях математики.
Суть его состоит в том, что отношения между дискретным и непрерывным, между языком и воображением, между алгеброй и топологией инвертируются. Непрерывность, геометрическое воображение, топология медленно завоевывают место первичного математического материала.
Язык становится вторичным, подчиненным, его «внутренняя письменность» возвращается к архаичной иероглифической форме, и его материей делается комбинаторика геометрических образов. Сама эта комбинаторика нелинейна, многомерна, и уже на уровне своего зарождения новый язык смешивает синтаксис, семантику и прагматику способами, которые мы еще не начали философски осмыслять.
Коммутативные диаграммы категорного языка были предвестием такой эволюции. С проникновением в обиход поликатегорий, обогащенных категорий, А∞-алгебр и подобных структур мы начинаем говорить на языке, который в гораздо меньшей степени поддается экстериоризации, чем мы привыкли.
Очень убедительным для меня аргументом в пользу того, что эта перцепция — больше, чем моя частная иллюзия, было осознание параллельных процессов, происходящих на границе математики с теоретической физикой. Я имею в виду Фейнмановские интегралы, методы ренормализации и такие их приложения, как интеграл Виттена, вычисляющий инварианты узлов.
* * *
В заключение я хочу вернуться к теме, с которой начал, — проблеме убедительности математики и, более общо, современной науки.
Убедительность личного опыта, свидетельств очевидцев, отсылка к авторитетам и авторитетным текстам часто воспринимаются как полный список средств убеждения. Конечно, физики, химики, биологи добавляют к этому списку направленный эксперимент.
Но я бы хотел рассмотреть здесь то, что я назову «цивилизационным» аргументом, интуитивно угаданным Коко Шанель. Цивилизация предоставляет в наше распоряжение способы проверки истинности, которые не сводятся ни к апелляции к авторитетам, ни к личному опыту разбора длинных математических доказательств, ни к свидетельствам.

Готовясь к этому докладу, я вел обильную переписку по электронной почте. Возможность ее воспринимается почти всеми сейчас как нечто, само собой разумеющееся. Но ее сделал возможной такой уровень математики, выстроенной за 2 тыс. лет, полномасштабную убедительность которого ни мы сами, ни авторитетные для нас люди проверить не в состоянии. Математика верна кроме всего прочего и потому, что открытие уравнений Максвелла привело к технике передачи информации электромагнитными волнами, а Булева алгебра стала работать в вашем и моем ноутбуке.
Культура математического рассуждения в цивилизационном аспекте есть важнейшая форма объективации абстрактного математического знания, способ его передачи от поколения к поколению.
В личностном плане математическую культуру, культуру доказательства я сравнил бы с тренировкой музыканта — отработка точности мелких движений, пока они не станут автоматическими и смогут быть синтезированными, скажем, в «Сонату для скрипки соло» Баха. Кодификация формального языка с его компонентами логики и теории множеств была идеальным средством такой «отработки точных движений». Но если она сопровождается идеологической пропагандой вроде интуиционизма или конструктивизма, она становится философски зашоренной и цивилизационную ценность теряет.
