Время от времени и наше скромное солнечно-гелиосферное научное сообщество встряхивает от необычных результатов и идей. Нам, конечно, далеко до ошеломляющих результатов высокой физики, но иногда и в нашем подернутом ряской заливчике плещутся волны. Само-то сообщество успокаивается довольно быстро, а вот в публичном пространстве волны бродят долго, сталкиваясь, искажаясь и деформируясь до неузнаваемости. Интерференция, в общем. Одной из таких встрясок оказалась недавно вышедшая статья Абрю и др. [1] о возможном влиянии планет на изменения солнечной активности, что, если окажется правдой, позволит делать далеко идущие предсказания и прогнозы. Этот результат произвел некий шум среди научной и околонаучной аудитории, имеющей косвенное отношение к солнечной физике. С другой стороны, реакция экспертов оказалась довольно вялой, в худшем случае сказать кратко — «Бред», в лучшем случае — пожать плечами и сказать, как мировая мама Жени Лукашина «Поживем, увидим». Я лично представляю лучший случай.
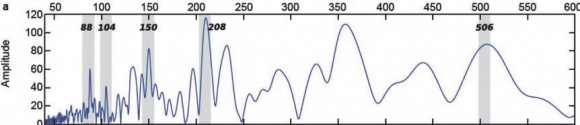
Так что же предложили миру Абрю сотоварищи? Используя временной ряд измерений космогенных изотопов в природных архивах в качестве индекса солнечной активности на шкале в 10 тысяч лет [2, 3], авторы выделили в нем несколько, как они называют, основных периодичностей, а именно 88, 104, 150, 208 и 506 лет. Затем они сосчитали гипотетическое изменение крутильного момента, вызванное гравитационным эффектом планет в области тахоклин (tachocline — узкая переходная область между дифференциально вращающейся конвективной зоной и квазитвердотельно вращающейся зоной лучевого переноса на Солнце) под действием взаимного положения планет, в довольно экзотических предположениях, нашли близкие частоты (см. рис. 1) и радостно сказали — ВОТ ОНО!
Давайте посмотрим на это ОНО «вооруженным» глазом. Выделение периодичностей в ряду солнечной активности сделано экзотическим способом:
- в скользящем временном окне выделялись, методом быстрого преобразования Фурье, 20 самых мощных спектральных линий;
- эти линии усреднялись по всем окнам с весом, равным не мощности, а рангу (от 1 до 20) линии в каждом окне;
- фаза не учитывалась вообще. Всякий, более-менее знакомый с выделением скрытых периодичностей, только пожмет плечами по поводу такого подхода.
Посмотрим на рис. 1 — пик на 208 годах хорошо известен как де-Ври/Зюсс цикл, пика 506 лет реально нет, да его ранее в тех же данных никто и не находил, зато он сильный в планетарных данных, пик в 104 года вообще нечестный — он не входит в «двадцатку» самых мощных и очевидно является гармоникой 208-летнего цикла, а куча прочих пиков просто проигнорирована. Таким образом, выделение периодичностей вызывает некоторые вопросы.
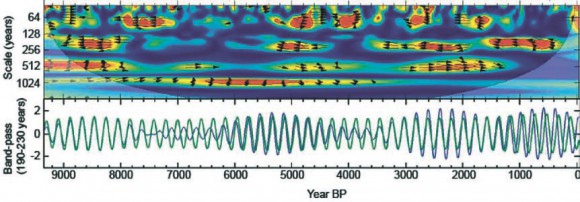
Идея планетарного влияния на солнечную активность известна давно, и обсуждается без особого успеха уже 150 лет. Еще в середине XIX века, после выявления 11-летней периодичности в вариациях солнечной активности, Рудольф Вольф предположил, что это — влияние Юпитера, орбитальный период которого чуть больше 11 лет. Однако, с тех пор эта идея так и не получила обоснования. Было предложено два механизма подобного воздействия — движение Солнца вокруг барицентра Cолнечной системы или приливные воздействия. Первый механизм нефизичен — барицентр удобная математическая точка, но физического притяжения к ней нет. Второй механизм слишком слабый, более того, приливные волны от дальних тяжелых планет пренебрежимо малы на Солнце по сравнению с близкими планетами. Запредельные гипотезы, вроде магнитного влияния планет на солнечное динамо или того, что солнечные пятна вызываются падением на Солнце комет, чьи орбиты возмущаются планетами, мы не рассматриваем. В данной работе авторы предложили новый механизм: если форма области тахоклина несферическая и сама область твердотельная, то планеты будут ее слегка закручивать своим гравитационным влиянием. Конечно, этот эффект ничтожен, но никто не знает, будет ли это играть роль. Никто не знает и форму тахоклина на глубине около 200 тыс. км под фотосферой — почему бы ей не быть несферической? Однако твердотельность вызывает больше скепсиса. Посмотрим на рис. 2 —вейвлет-когерентность между солнечной активностью и крутильным моментом, вызванным планетами на твердую несферическую область тахоклина. Устойчивый 208-летний цикл показывает четкую обратную связь — фазовый сдвиг 180 градусов. Однако, на 506 годах сигналы уже синфазны, а на временной шкале около сотни лет их взаимная фаза плавает.
Что мы имеем в итоге? Периодичности выделены нестандартным методом, механизм предложен только качественный без надежды оценить эффект количественно в ближайшем будущем, и, наконец, эффект меняется от положительного на отрицательный на разных временных шкалах. Думаю, еще рановато говорить о разгадке долговременных изменений солнечной активности.
1. Abreu, J. A. et al., Is there a planetary infuence on solar activity? Astron. Astrophys., 548, A88, 2012.
2. Usoskin, I., A History of Solar Activity over Millennia, Living Rev. Solar Phys., 5, 3, 2008.
3. Beer, J., K. McCracken and R. von Steiger, Cosmogenic Radionuclides: Theory and Applications in the Terrestrial and Space Environments, Springer Verlag, Berlin Heidelberg, 2012.

Илья, добрый день!
Спасибо за интересную заметку.
С учётом того, что высота приливного горба пропорциональна квадрату отношения радиуса Солнца к расстоянию до Юпитера, а квадрупольное число Лява h_2 не превышает 5/2, гипотеза Рудольфа Вольфа представляется очень спорной.
Отважусь задать вопрос по поводу гипотетической твёрдости тахоклинной зоны. Заранее извиняюсь, если вопрос окажется наивным (я не специалист по звёздам).
Peter Williams и независимо от него Gordon Ogilvie со товарищи опубликовали несколько работ о так называемой магнитной жёсткости звёзд. Говоря вульгарно, плазма “прилипает” к магнитным линиям, и среда обретает эффективные модули жёсткости. Применимо ли это построение к Солнцу вообще и к тахоклинной зоне в частности (или к объёму ниже этой зоны)? Ещё раз прошу прощения, если вопрос тривиален.
С Новым Годом и Рождеством,
Михаил