
В последнее время появилось довольно много работ, посвященных проблеме пробок в Москве. Мэр Москвы объявил борьбу с пробками одним из главных приоритетов, руководитель департамента транспорта, согласно «Ведомостям», круглосуточно наблюдает за дорогами в планшете, а в Генплане делают подробную модель транспортной системы Москвы. Александр Гасников (МФТИ), Юрий Дорн (МФТИ, НИиПИ Генплана Москвы), Андрей Прохоров и Владимир Швецов (А+С Консалт) рассказывают о тех подходах, которые могут предложить ученые к решению этих проблем.
На наш взгляд приоритеты и меры борьбы с пробками выбираются всё более адекватные. Однако, как правило, именно эффективные методы встречают сопротивление со стороны населения, а поддержкой пользуются в основном сомнительные инициативы. В этой статье мы хотели бы поговорить о мерах борьбы с пробками и их действенности (более строгое с математической точки зрения изложение можно найти в книге «Введение в математическое моделирование транспортных потоков» [1]).
Откуда берутся пробки?
Продемонстрируем «на пальцах» одну из причин возникновения пробок, важную в дальнейшем. Предположим, что у нас поток в 2000 автомобилей в час из пункта А в пункт Б. Причем из А в Б ведут две дороги (маршрута). Первая дорога — «быстрая», путь занимает 20 минут (если нет пробок), но по ней может проехать не более 1200 автомобилей в час. Вторая же дорога — «объезд», на нем тоже может проехать 1200 автомобилей в час, но уже за 40 минут. Понятно, что сначала все водители попробуют проехать по «быстрой» дороге. Но она не способна обслужить весь поток. Начнет образовываться очередь (пробка).
С ростом числа автомобилей в пробке будет увеличиваться и время проезда по данной дороге для новоприбывших автомобилистов. В какой-то момент некоторым из пользователей покажется, что пробка так разрослась, что выгоднее ехать в объезд. Причем на объезде все поедут свободно. Так мы получим равновесие, при котором обе альтернативы сулят одинаковый выигрыш (ну или проигрыш). Понятно, что именно эгоизм водителей мешает сразу распределить трафик так, чтобы все лишние машины поехали в объезд. Пробка — плата за эгоизм. Ее роль — уравнять выигрыши на используемых альтернативах.
Всегда ли выгодно строить новые дороги?
Почему строительство новых дорог не всегда улучшает ситуацию с пробками и способно даже усугубить проблему? Есть два важных соображения на этот счет. Воспользуемся следующей простой моделью.
Представим пользователей (не только водителей) транспортной инфраструктуры в качестве игроков, которые выбирают сначала тип транспорта, а затем подходящий маршрут и стараются минимизировать свои издержки на проезд. Под издержками мы понимаем не только время в пути, но и комфортность передвижения, а также финансовые и другие затраты водителей. Тогда мы получим обычную игру, для решения которой нужно найти равновесие. Это равновесие носит имя Нэша — Вардропа. Интересно, что система «скатывается» в него, даже если водители не умеют точно оценивать ситуацию на дороге, но при этом могут «учиться» со временем. Это стандартный результат эволюционной теории потенциальных игр. Желающих познакомиться с игровой постановкой поближе мы отсылаем к статье Вильяма Сэндхольма [2], а сейчас вернемся к нашим водителям.
Соображение первое: издержки водителей определяются из условия равновесия между личным и общественным транспортом.
Строительство новых дорог приводит (обычно, но не всегда) к увеличению пропускной способности транспортной сети и к снижению средних (временных) издержек водителей. Если бы все жители использовали только личные транспортные средства, то цель была бы достигнута — среднее время в пути при строительстве новых дорог скорее всего снизилось бы. Однако транспортная система включает также общественный транспорт, пользователи которого зачастую имеют автомобиль или могут позволить себе его покупку.
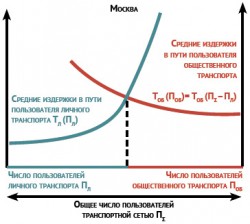
Посмотрим на то, как друг на друга влияют общественный и личный транспорт. В равновесии издержки (среднее время в пути с учетом комфортности передвижения) для водителей личного и пользователей общественного транспорта равны (см. рис. 1). Причем не так уж важно то, что не все пользователи общественного транспорта могут позволить себе автомобиль. Важно лишь то, чтобы автомобилем владели или могли владеть достаточное их количество (что, вообще говоря, и наблюдается).
Допустим, что строительство дорог приведет к исчезновению пробок и существенному снижению времени проезда на личном транспорте. Это соответствует сдвигу графика издержек для личного транспорта «вправо» (если не наблюдается аномалий, таких, как парадокс Браесса, о котором мы будем говорить ниже). Но тогда пассажирам общественного транспорта, имеющим автомобиль, становится выгодно вновь начать его использовать. В свою очередь изменение их решения приведет к увеличению числа автомобилистов, что вызовет появление пробок и, следовательно, увеличению времени в пути. Система «скатится» в новое равновесие, в котором издержки при использовании общественного и личного транспорта вновь совпадут. Конечно, в среднем мы (обычно) выигрываем, но куда меньше, чем ожидалось. Доступная альтернатива — улучшать общественный транспорт. Это соответствует сдвигу графика издержек общественного транспорта «вниз». В равновесии издержки на общественном и личном транспорте равны, а значит, улучшая общественный транспорт и привлекая на него больше людей, ранее использовавших автомобиль, мы разгружаем дороги и улучшаем ситуацию во всей транспортной системе. Конечно, строительство дорог работает обычно в том же ключе. Но оно несравнимо дороже.
Соображение второе: иногда выгоднее закрывать дороги, а не строить новые.
Еще в 60-х годах прошлого столетия немецкий математик Дитрих Браесс привел пример сети, в которой строительство новой дороги приводило к увеличению издержек (времени проезда) для всех участников дорожного движения [3]. Данный контр интуитивный пример был назван парадоксом его имени. Буквально через год было показано, что он наблюдается в реальных сетях. В частности, неэффективные дороги нашли в Германии, позднее в США и ряде других стран. Совсем недавно парадокс Браесса был выявлен во Владивостоке. Более того, как показали Роугарден и Вэлиант [4], данный парадокс встречается с большой вероятностью в случайных графах, то есть в случайно построенных транспортных сетях.
Может показаться, что проблема надуманна, и достаточно найти неэффективные ребра в имеющейся сети, убрать их и правильно строить дороги в дальнейшем. Однако всё сложнее. Ранее Роугарден показал [5], что даже при достаточно общих предположениях о свойствах транспортной сети поиск неэффективных ребер является NP-сложной задачей, то есть фактически не решаемой. С другой стороны, как показал Мильтах, единственная сеть, в которой не может реализоваться парадокс Браесса, — это сеть параллельных дорог. Всё это говорит о том, что непродуманное увеличение числа дорог может не только не улучшить ситуацию, но даже ухудшить ее, причем для всех участников дорожного движения.
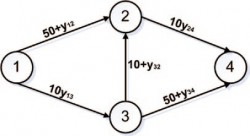
Модельный пример см. на рис. 2.
Из 1 в 4 в единицу времени выезжает 6 автомобилей. Буквой y обозначается количество автомобилей, проезжающих по данному ребру в единицу времени, формулы над ребрами — веса ребер (время проезда ребра в минутах в зависимости от величины потока автомобилей по ребру y). Условие равновесия: все используемые пути должны иметь одинаковую «длину». Всего путей, ведущих из 1 в 4 три: 1—3—4, 1—3—2—4, 1—2—4.
Легко проверить, что если эти 6 автомобилей в одинаковых пропорциях распределятся по всем этим путям (по 2 автомобиля в единицу времени на каждый путь), то время прохождения каждого пути («длина» пути) будет равна 92 минутам (10·(2+2)+(50+2) = 10·(2+2)+(10+2)+10·(2+2) = (50+2)+10·(2+2)). Это и будет единственным равновесием (Нэша — Вардропа) в транспортной сети. То есть от такой конфигурации никому из водителей не выгодно отклоняться при условии, что остальные водители не меняют свой выбор.
Однако если ребро (дорогу) 3—2 перекрыть, то единственной равновесной конфигурацией будет по 3 автомобиля в единицу времени на пути 1—3—4 и 1—2—4. Время в пути будет 10·3+(50+3) = (50+3)+10·3 = 83 минуты. То есть всем стало лучше! Примечательно, что если предложить людям играть в такую повторяющуюся игру (мы проводили такой эксперимент со студентами Физтеха), в которой выбор маршрута следования определяется каждым игроком на основе предыдущих розыгрышей, то система действительно сходится в равновесие Нэша — Вардропа в обоих случаях (с дорогой 3—2 и без нее).
Социальный оптимум и как его достичь?
Было обнаружено, что во многих реальных транспортных сетях типичной является следующая ситуация. Возникающее равновесное распределение потоков (равновесие Нэша — Вардропа) довольно далеко от того, чего можно достичь в социальном оптимуме, то есть в лучшем, с точки зрения общества, случае (см., например, рис. 2). Социальный оптимум можно достичь, если централизовано управлять выбором пути каждого водителя. Другой способ — оптимальное взимание платы за проезд с дорог.
В перспективе плату за проезд по дорогам можно будет рассчитывать исходя из информации о треках автомобилей. Можно оснастить все автомобили GPS или ГЛОНАСС-навигаторами, позволяющими определять каждые 5 минут положение автомобиля с точностью до нескольких метров. Каждая дорога имеет свой тариф: за проезд по дороге начисляется плата, подобно плате за разговор по мобильному телефону. В конце месяца приходит счет. Этот же механизм позволяет вводить и субсидии для некоторых дорог.
Можно показать, что при весьма общих условиях существует такой способ взимания платы за проезд, который приводит к социальному оптимуму. В основе этого подхода лежит метаигровой синтез: меняя «правила игры» (вводя платы за проезд определенным образом) можно так подобрать эти «правила», чтобы социальной оптимум в задаче без платных дорог соответствовал (устойчивому) равновесию Нэша — Вардропа (т.е. транспортная система со временем именно в это равновесие и приходит) в задаче с платными дорогами. Мировой опыт (например, Сингапура) подсказывает, что потенциально это очень эффективный и малозатратный способ «выжать максимум» из имеющейся транспортной сети при сложившихся потребностях в перемещениях (матрице корреспонденций).
Зачем нужны и чем важны выделенные полосы?
Вернемся к идее «пересаживания» водителей с личного транспорта на общественный. Хотелось бы пересаживать водителей на общественный транспорт с помощью рыночных механизмов. Например, регулируя цену на топливо и стоимость проезда в общественном транспорте. В частности, вводя большие платы за проезд по дорогам на личном транспорте или повышая цену на топливо и удерживая цену за проезд на общественном транспорте можно сделать использование личного транспорта совершенно невыгодным — понятно, что это плохие способы решения проблемы.
Другой, более адекватный, способ — выделенные полосы. Ужесточение штрафов за неправильную парковку. Платные парковки. Именно по этому пути сейчас идет развитие Москвы. Расчеты показали, что симбиоз указанных способов при весьма общих условиях позволяет оптимальным образом расщеплять транспортные потоки, причем это можно делать адаптивно. Но не менее важно здесь и то, что эффект от этого расщепления оказывается наиболее значимым по сравнению со многими другими способами быстро побороть пробки в Москве. Другими словами, выбранный в Москве путь, связанный с попыткой оптимально перераспределить потоки между личным и общественным транспортом, выглядит, на наш взгляд, вполне оптимистичным. Конечно, любая из указанных мер при бездумном применении может не помочь, а усугубить ситуацию. Именно по этому важно уметь просчитывать эффекты от тех или иных мер заранее.
Компьютерное моделирование транспортных потоков
Необходимо отметить, что все транспортные и социально-экономические последствия внедрения тех или иных мер на транспортной сети можно и нужно оценивать. Особую роль здесь играют прикладные (компьютерные) транспортные модели, которые, как правило, являются основным инструментальным средством городского транспортного планирования.
Такие модели интегрируют разнообразные данные о транспортном спросе и предложении и помогают путем сравнения расчетов множества вариантов принимать решения относительно развития транспортной инфраструктуры. То есть мы можем путем численного моделирования сравнивать издержки пользователей в равновесиях и смотреть, какой проект приводит к наименьшим средним издержкам.
Важным преимуществом использования компьютерных транспортных моделей становится возможность рассмотрения и количественной оценки всей транспортной системы. Это важно, так как всегда есть выбор из множества инфраструктурных проектов, и необходимо понять, какой из них стоит реализовывать.
Использование комплексных моделей, учитывающих различные типы транспорта и предпочтения населения, позволяет оценивать проекты и ранжировать их. Также возможно (с помощью той же методологии сравнения равновесий) оценивать не только инфраструктурные проекты, но и практически любое воздействие на транспортную систему, будь то введение платы за проезд или запрет на въезд в центр города. Существуют и другие методологии по количественной оценке проектов.
На настоящий момент не существует единой утвержденной методики оценки эффективности транспортных инвестиционных проектов во взаимоувязке с транспортным моделированием. При этом методологии, имеющие какой-либо правовой статус в России (т.е. использование которых предписывается или рекомендуется тем или иным законодательным актом), либо неполны, либо устарели.
Также стоит отметить, что наиболее серьезная проблема при построении таких комплексных моделей — недостаток данных, требуемых для их калибровки.
Почему в большинстве крупных городов есть пробки?
Пусть имеется некоторый крупный город. Задан граф транспортной сети этого города с хорошими показателями связности, доступности, надежности. Тогда, если мы введем среднее число автомобилей, находящихся на транспортном графе, и станем плавно это число менять, то будем наблюдать довольно резкий и масштабный спад времени в пути среднестатистического пользователя в малой окрестности некоторого порогового значения. Этот феномен наблюдается в целом ряде различных моделей (TASEP типа, на основе сетей Джексона и др.). Иногда в этом контексте говорят о фазовом переходе.
Математически строго это можно показать лишь в самых простых (модельных) случаях (см., например, приложения Бланка и Замятина — Малышева в учебном пособии, упоминаемом выше [1]). Однако можно поставить численный эксперимент. По мнению В. П. Мартынова (ЦОДД) для Москвы критическое значение лежит в диапазоне 450–500 тыс. автомобилей. Другими словами, если сейчас, в данный конкретный момент, на дорогах Москвы меньше 450 тыс. автомобилей, то заторы практически отсутствуют, Яндекс.Пробки показывают 3–4 балла и все счастливы. Если же число автомобилей увеличится до 500 тыс., то практически все они стоят в заторах. Обсуждаемый резкий рост загруженности дорог в зависимости от числа пользователей (для личного транспорта) хорошо виден на соответствующем графике рис. 1.
Тем не менее, типичным также будет наличие определенной довольно большой доли ребер графа транспортной сети, загрузка которых практически не чувствительна к такому увеличению. В действительности многие крупные города как раз находятся где-то на границе этого «фазового перехода». Причина проста и имеет в своей основе принцип неподвижной точки в форме теоремы Брауэра.
Если рассматривать эволюцию города с точки зрения появления новых жителей, новых рабочих мест, строительства новых дорог, то можно условно считать, что новый житель будет пользоваться личным автомобилем в городе, если выигрыш от пользования не ниже некоторого уровня, определяемого, например, выигрышем от использования альтернативы в виде общественного транспорта. Поскольку в малой окрестности критического значения происходит резкое увеличение издержек для личного транспорта (см. рис. 1), то у большинства новых потенциальных пользователей транспортной сети пропадает желание использовать автомобиль. Аналогично можно пойти и в обратную сторону.
Идеи развития общественного транспорта с целью улучшения всей транспортной сети не новы и вполне естественны. О них можно прочитать в научно-популярной книге Вукана Вучека «Транспорт в городах, удобных для жизни» [6] или в переводе лекции Фила Гудвина на «Полит.ру» [7]. Мы лишь пытались подчеркнуть, что основные тезисы, содержащиеся в этих работах и в нашей статье, опираются не только на интуицию, но и на математические модели, пусть иногда и простые.
1. Гасников А.В., Кленов С.Л., Нурминский Е.А., Холодов Я.А., Шамрай Н.Б. Введение в математическое моделирование транспортных потоков. М.: МЦНМО, 2012.
2. Sandholm W., Evolutionary Implementation and Congestion Pricing, Review of Economic Studies, 2002, V.69, P. 667—689.
3. Braess D. Über ein Paradoxon aus der Verkehrsplanung, Unternehmensforschung, 1969, V. 12, P. 258–268.
4. Valiant G. and Roughgarden T. Braess’s Paradox in Large Random Graphs, Random Structures and Algorithms, 2010, V.37, P.495—515.
5. Roughgarden T. On the severity of Braess’s Paradox: Designing networks for selfsh users is hard, Journal of Computer and System Sciences, 2006, V.72, P.922—953
6. Вукан Р. Вучик. Транспорт в городах, удобных для жизни. М.: Изд-во «Территория будущего», 2011. В оригинале: Vukan R. Vuchic. Transportation for Livable Cities.
7. Решение проблемы пробок. Лекция британского ученого-транспортника Фила Гудвина (Phil Goodwin) в переводе М. Блинкина. 2009. www.polit.ru/article/2009/03/24/probki/